【题目】某校为美化校园,计划对面积为1800平方米区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400平方米区域绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积分别是多少平方米?
参考答案:
【答案】解:设乙工程队每天能完成绿化面积是x平方米,则甲工程队每天能完成绿化面积是2x平方米, 根据题意得: ![]() ﹣
﹣ ![]() =4,
=4,
解得:x=50,
经检验,x=50是原方程的解,
∴2x=100.
答:甲、乙两工程队每天能完成绿化的面积分别是100平方米、50平方米
【解析】设乙工程队每天能完成绿化面积是x平方米,则甲工程队每天能完成绿化面积是2x平方米,根据时间=工作总量÷工作效率结合“在独立完成面积为400平方米区域绿化时,甲队比乙队少用4天”,即可得出关于x的分式方程,解之经检验后即可得出结论.
【考点精析】利用分式方程的应用对题目进行判断即可得到答案,需要熟知列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两个全等三角形拼成一个菱形,则这两个三角形的形状一定是( )
A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)1﹣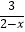 =
= 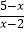 ;
;
(2)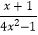 =
= 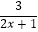 ﹣
﹣ 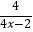 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,作出函数
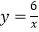 的图象,并根据图象回答下列问题:
的图象,并根据图象回答下列问题: 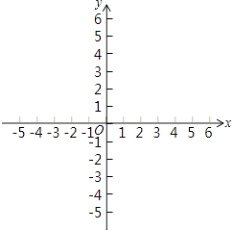
(1)当x=﹣2时,求y的值;
(2)当2<y<4时,求x的取值范围;
(3)当﹣1<x<2,且x≠0时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
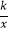 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n). 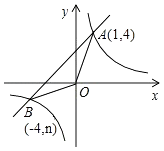
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有( )
①AP=BP; ②2BP=AB; ③AB=2AP; ④AP+PB=AB.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
相关试题

