【题目】已知:如图,四边形ABCD中,AD∥BC,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD,DB=DE。
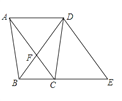
(1)求证:四边形ACED是平行四边形;
(2)联结AE,交BD于点G,求证: ![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)证△ABD≌△CDE,推出AD=CE,由AD∥CE,即可推出结论;(2)根据平行得出比例式,再根据比例式的性质进行变形,即可得出答案.
本题解析:证明:(1)∵梯形ABCD,AD∥BC,AB=CD,
∴∠BAD=∠CDA,∵AD∥BE, ∴∠ADC=DCE, ∴∠DAB=DCE
在△BAD和△CDA中
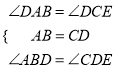
∴△ABD≌△CDE,∴AD=CE
又∵AD∥CE,∴∠ACD=∠CDE,
∴四边形ACED是平行四边形;
(2) ∵四边形ACED是平行四边形,∴FC∥DE, ∴![]() , ∵AD∥BE,
, ∵AD∥BE,
∴![]() ,又∵AD=CE, ∴
,又∵AD=CE, ∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+ax+b=0有一个非零根-b , 则a-b的值为( )
A.1
B.-1
C.0
D.-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点P(﹣1,4)向右平移2个单位长度后,再向下平移3个单位长度,得到点P1,则点P1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C(3,6),则点B(﹣5,﹣2)的对应点D的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(3x+4)(3x﹣4)﹣x(x﹣4)>8(x+1)2 , 并把它的解集在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
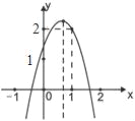
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
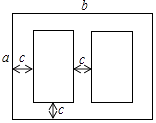
(1)用代数式表示这两个篮球场的占地面积.
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
相关试题

