Question

【题目】如图，Rt△ABC中，∠ACB=90°，AC=BC，点D、E在边AB上，且∠DCE=45°

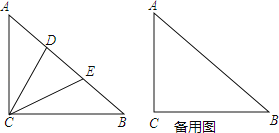
（1）以点C为旋转中心，将△ADC顺时针旋转90°，画出旋转后的图形；

（2）若AD=2，BE=3，求DE的长；

（3）若AD=1，AB=5，直接写出DE的长．

Answer 1

【答案】（1）见解析；（2）DE=；（3）DE的长为．

【解析】

试题分析：（1）利用旋转的性质作图；

（2）连结EF，如图，先根据等腰直角三角形的性质得∠A=∠ABC=45°，再根据旋转的性质得CD=CF，BF=AD=2，∠DCF=90°，∠CBF=∠A=45°，则可根据“SAS”判断△DCE≌△FCE，得到DE=FE，然后在△BEF中利用勾股定理计算EF，从而得到DE的长；

（3）设ED=x，则BE=4﹣x，由（2）的证明得到EF=DE=x，BF=AD=1，然后在Rt△BEF中利用勾股定理得到12+（4﹣x）2=x2，再解方程即可．

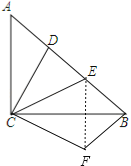
解：（1）如图，△BCF为所作；

（2）连结EF，如图，

∵∠ACB=90°，AC=BC，

∴∠A=∠ABC=45°，

∵△ADC顺时针旋转90°得到△BCF，

∴CD=CF，BF=AD=2，∠DCF=90°，∠CBF=∠A=45°，

∵∠DCE=45°，

∴∠FCE=45°，

在△DCE和△FCE中

，

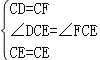∴△DCE≌△FCE，

∴DE=FE，

在△BEF中，∵∠EBC=45°，∠CBF=45°，

∴∠EBF=90°，

∴EF==，

∴DE=；

（3）∵AD=1，AB=5，

∵BD=4，

设ED=x，则BE=4﹣x，

由（2）得EF=DE=x，BF=AD=1，

在Rt△BEF中，12+（4﹣x）2=x2，解得x=，

即DE的长为．