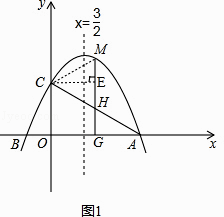
【题目】如图,在平面直角坐标系中,抛物线y=ax2+ ![]() x+c(a≠0)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x=
x+c(a≠0)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x= ![]() .
.
(1)求抛物线的解析式;
(2)M为第一象限内的抛物线上的一个点,过点M作MG⊥x轴于点G,交AC于点H,当线段CM=CH时,求点M的坐标;
(3)在(2)的条件下,将线段MG绕点G顺时针旋转一个角α(0°<α<90°),在旋转过程中,设线段MG与抛物线交于点N,在线段GA上是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵x=﹣ ![]() =
= ![]() ,b=
,b= ![]() ,
,
∴a=﹣ ![]() ,
,
把A(4,0),a=﹣ ![]() 代入y=ax2+
代入y=ax2+ ![]() x+c,
x+c,
可得( ![]() )×42+
)×42+ ![]() ×4+c=0,
×4+c=0,
解得c=2,
则抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:如图1,连接CM,过C点作CE⊥MH于点E,
 ,
,
∵y=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
∴当x=0时,y=2,
∴C点的坐标是(0,2),
设直线AC解析式为y=kx+b(k≠0),
把A(4,0)、C(0,2)代入y=kx+b,
可得 ![]() ,
,
解得: 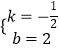 ,
,
∴直线AC解析式为y=﹣ ![]() x+2,
x+2,
∵点M在抛物线上,点H在AC上,MG⊥x轴,
∴设点M的坐标为(m,﹣ ![]() m2+
m2+ ![]() m+2),H(m,﹣
m+2),H(m,﹣ ![]() m+2),
m+2),
∴MH=﹣ ![]() m2+
m2+ ![]() m+2﹣(﹣
m+2﹣(﹣ ![]() m+2)=﹣
m+2)=﹣ ![]() m2+2m,
m2+2m,
∵CM=CH,OC=GE=2,
∴MH=2EH=2×[2﹣(﹣ ![]() m+2)]=m,
m+2)]=m,
又∵MH=﹣ ![]() m2+2m,
m2+2m,
∴﹣ ![]() m2+2m=m,
m2+2m=m,
即m(m﹣2)=0,
解得m=2或m=0(不符合题意,舍去),
∴m=2,
当m=2时,
y=﹣ ![]() ×22+
×22+ ![]() ×2+2=3,
×2+2=3,
∴点M的坐标为(2,3)
(3)
解:存在点P,使以P,N,G为顶点的三角形与△ABC相似,理由为:
∵抛物线与x轴交于A、B两点,A(4,0),A、B两点关于直线x= ![]() 成轴对称,
成轴对称,
∴B(﹣1,0),
∵AC= ![]() =2
=2 ![]() ,BC=
,BC= ![]() =
= ![]() ,AB=5,
,AB=5,
∴AC2+BC2= ![]() +
+ ![]() =25,AB2=52=25,
=25,AB2=52=25,
∵AC2+BC2=AB2=25,
∴△ABC为直角三角形,
∴∠ACB=90°,
线段MG绕G点旋转过程中,与抛物线交于点N,当NP⊥x轴时,∠NPG=90°,
设P点坐标为(n,0),
则N点坐标为(n,﹣ ![]() n2+
n2+ ![]() n+2),
n+2),
①如图2,
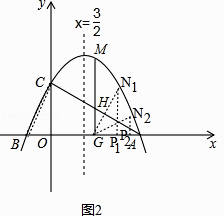
当 ![]() =
= ![]() 时,
时,
∵∠N1P1G=∠ACB=90°,
∴△N1P1G∽△ACB,
∴ ![]() =
= ![]() ,
,
解得:n1=3,n2=﹣4(不符合题意,舍去),
∴P的坐标为(3,0).
②当 ![]() =
= ![]() 时,
时,
∵∠N2P2G=∠BCA=90°,
∴△N2P2G∽△BCA,
∴ ![]() ,
,
解得:n1=1 ![]() ,n2=1﹣
,n2=1﹣ ![]() (不符合题意,舍去),
(不符合题意,舍去),
∴P的坐标为(1+ ![]() ,0).
,0).
∴存在点P(3,0)或(1 ![]() ,0),使以P,N,G为顶点的三角形与△ABC相似.
,0),使以P,N,G为顶点的三角形与△ABC相似.
【解析】(1)首先利用对称轴公式求出a的值,然后把点A的坐标与a的值代入抛物线的解析式,求出c的值,即可确定出抛物线的解析式.(2)首先根据抛物线的解析式确定出点C的坐标,再根据待定系数法,确定出直线AC解析式为y=﹣ ![]() x+2;然后设点M的坐标为(m,﹣
x+2;然后设点M的坐标为(m,﹣ ![]() m2+
m2+ ![]() m+2),H(m,﹣
m+2),H(m,﹣ ![]() m+2),求出MH的值是多少,再根据CM=CH,OC=GE=2,可得MH=2EH,据此求出m的值是多少,再把m的值代入抛物线的解析式,求出y的值,即可确定点M的坐标.(3)首先判断出△ABC为直角三角形,然后分两种情况:①当
m+2),求出MH的值是多少,再根据CM=CH,OC=GE=2,可得MH=2EH,据此求出m的值是多少,再把m的值代入抛物线的解析式,求出y的值,即可确定点M的坐标.(3)首先判断出△ABC为直角三角形,然后分两种情况:①当 ![]() =
= ![]() 时;②当
时;②当 ![]() =
= ![]() 时;根据相似三角形的性质,判断出是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似即可.
时;根据相似三角形的性质,判断出是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=
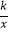 (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= 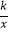 (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 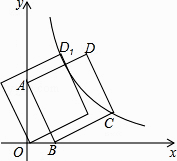
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个仓库共存有粮食60
 .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:(1)甲仓库运进粮食14
 ,乙仓库运出粮食10
,乙仓库运出粮食10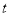 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?(2)如果甲仓库原有的粮食比乙仓库的2倍少3
 ,则甲仓库运出多少
,则甲仓库运出多少 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等? (3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1
 ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣1,0,1,2这5个数中,随机抽取一个数记为a,则使关于x的不等式组
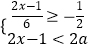 有解,且使关于x的一元一次方程
有解,且使关于x的一元一次方程 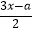 +1=
+1= 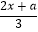 的解为负数的概率为 .
的解为负数的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知G、H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG、FH交于点D,连接AD、DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
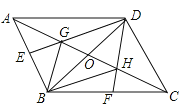
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )

A. 南偏东30° B. 北偏东30° C. 南偏东 60° D. 南偏西 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC的垂直平分线分别交AB,CD于点E,F,连接AF,CE,如果∠BCE=26°,则∠CAF=_____

相关试题

