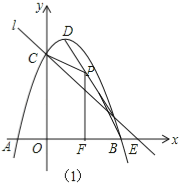
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
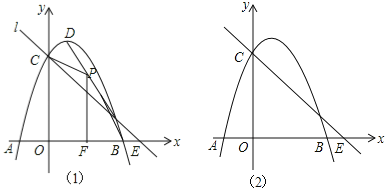
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
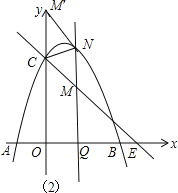
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)D(1,4),y=﹣![]() x+3(2)当x=
x+3(2)当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;(3)存在,(
;(3)存在,(![]() ,0)或(4,0)
,0)或(4,0)
【解析】
试题分析:(1)先把抛物线解析式配成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先根据抛物线与x轴的交点问题求出B(3,0),再利用待定系数法求出直线BD的解析式为y=﹣2x+6,则P(x,﹣2x+6),然后根据梯形的面积公式可得S=﹣x2+![]() x(1≤x≤3),再利用而此函数的性质求S的最大值;
x(1≤x≤3),再利用而此函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则可表示出M(t,﹣![]() t+3),N(t,﹣t2+2t+3),利用两点间的距离公式得到MN=|t2﹣
t+3),N(t,﹣t2+2t+3),利用两点间的距离公式得到MN=|t2﹣![]() t|,CM=
t|,CM=![]() t,然后证明NM=CM得到|t2﹣
t,然后证明NM=CM得到|t2﹣![]() t|=
t|=![]() t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),
当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线l的解析式为y=kx+b,
把C(0,3),E(4,0)分别代入得![]() ,解得
,解得 ,
,
∴直线l的解析式为y=﹣![]() x+3;
x+3;
(2)如图(1),当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),
设直线BD的解析式为y=mx+n,
把B(3,0),D(1,4)分别代入得![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=﹣2x+6,
则P(x,﹣2x+6),
∴S=![]() (﹣2x+6+3)
(﹣2x+6+3)![]() x=﹣x2+
x=﹣x2+![]() x(1≤x≤3),
x(1≤x≤3),
∵S=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(3)存在.
如图2,设Q(t,0)(t>0),则M(t,﹣![]() t+3),N(t,﹣t2+2t+3),
t+3),N(t,﹣t2+2t+3),
∴MN=|﹣t2+2t+3﹣(﹣![]() t+3)|=|t2﹣
t+3)|=|t2﹣![]() t|,
t|,
CM=![]() =
=![]() t,
t,
∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,
而QN∥y轴,
∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,
∴∠M′CN=∠CNM,
∴∠M′CN=∠CNM′,
∴CM′=NM′,
∴NM=CM,
∴|t2﹣![]() t|=
t|=![]() t,
t,
当t2﹣![]() t=
t=![]() t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
当t2﹣![]() t=﹣
t=﹣![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,0),
,0),
综上所述,点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组):
(1)10(x﹣3)﹣4≤2(x﹣1)
(2)x﹣
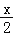 ﹣
﹣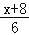 <1﹣
<1﹣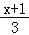
(3)
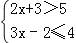
(4)
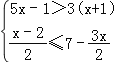 (在数轴上表示解集)
(在数轴上表示解集) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为18,BD=2DC,AE=EC,那么阴影部分的面积是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司最近开发A、B两种型号的手机,一经营手机专卖店销售A、B两种型号的手机,上周销售1部A型3部B型的手机,销售额为8400元.本周销售2部A型1部B型的手机,销售额为5800元.
(1)求每部A型和每部B型手机销售价格各是多少元?
(2)如果某单位拟向该店购买A、B两种型号的手机共6部,发给职工联系业务,购手机费用不少于11200元且不多于11600元,问有哪几种购买方案?
(3)在(2)中哪种方案费用更省?最少费用是多少?
-
科目: 来源: 题型:
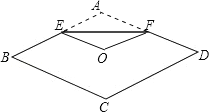
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF= cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2+bx+c(a≠0)的图象上有两点,坐标分别为(x1 , y1),(x2 , y2),其中x1<x2 , y1y2<0,则下列判断正确的是( )
A.a<0
B.a>0
C.方程ax2+bx+c=0必有一根x0满足x1<x0<x2
D.y1<y2
相关试题

