Question

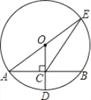
【题目】如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（ ）

A. 2 B. 8 C. 2 D. 2

Answer 1

【答案】D

【解析】连结BE，设⊙O的半径为R，由OD⊥AB，根据垂径定理得AC=BC=AB=4，在Rt△AOC中，OA=R，OC=R-CD=R-2，根据勾股定理得到（R-2）2+42=R2，解得R=5，则OC=3，由于OC为△ABE的中位线，则BE=2OC=6，再根据圆周角定理得到∠ABE=90°，然后在Rt△BCE中利用勾股定理可计算出CE．

解：连结BE，设⊙O的半径为R，如图所示，

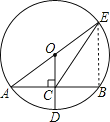
∵OD⊥AB，

∴AC=BC=AB=×8=4，

在Rt△AOC中，OA=R，OC=R-CD=R-2，

∵OC2+AC2=OA2，

∴（R-2）2+42=R2，解得R=5，

∴OC=5-2=3，

∴BE=2OC=6，

∵AE为直径，

∴∠ABE=90°，

在Rt△BCE中，．

考点: 1.垂径定理；2.勾股定理；3.三角形中位线定理；4.圆周角定理．

“点睛”本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．