Question

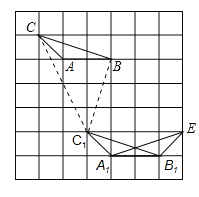
【题目】如图，△ABC的顶点A、B、C都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形，试在方格纸上按下列要求画格点三角形：

（1）将△ABC先向下平移4个单位，再向右平移2个单位得到△A1B1C1；

（2）线段AC与A1C1的关系 ；

（3）画AC边上的高线BE；（利用网格点和直尺画图）

（4）连接CC1，则∠BCC1＝ °．

Answer 1

【答案】（1）见解析；（2）AC∥A1C1 ，AC=A1C1；（3）见解析；（4）45

【解析】

（1）将A、B、C按平移条件找出它们的对应点，顺次连接，即得到平移后的图形；

（2）根据平移的性质即可求解；

（3）根据网格的特点及高的定义即可求解；

（4）连接BC1，利用勾股定理的逆定理得出△BCC1是等腰直角三角形进而求出∠BCC1．

（1）如图，△A1B1C1为所求；

（2）∵平移，∴AC∥A1C1 ，AC=A1C1，

故答案为：AC∥A1C1 ，AC=A1C1

（3）如图，BE为所求；

（4）连接BC1，

∵BC＝，BC1＝，CC1＝，

∴BC2＋BC12=C1C2，

∴△BCC1是等腰直角三角形，

∴∠BCC1＝45°．

故答案为：45．