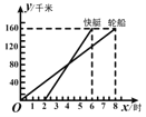
【题目】如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t(时)变化的图象,根据图象回答下列问题
(1)轮船的行驶速度是___________km/h;
(2)当2≤t≤6时,求快艇行驶过程y与t的函数关系式;
(3)当快艇与乙港相距40 km时,快艇和轮船相距___________km
参考答案:
【答案】(1)20;(2)![]() ;(3)20;
;(3)20;
【解析】
(1)根据速度=路程÷时间即可求得轮船行驶的速度;
(2) 设表示快艇行驶过程的函数式为y=kt+b,根据图象找出点的坐标利用待定系数法即可求出函数解析式;
(3)根据快艇与乙港相距40 km算出轮船行驶的时间,再根据(1)轮船的速度计算出此时轮船行驶的路程,再做减法即可得到答案;
解:(1)从图象可以得到,轮船行驶160千米所需的时间为8小时,
所以轮船的速度为:![]() km/h;
km/h;
故答案为:![]() km/h;
km/h;
(2) 设表示快艇行驶过程的函数式为y=at+b,
根据图象可知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() ,解得:
,解得:![]() ,
,
故快艇行驶过程y与t的函数关系式为:![]() ;
;
(3)由(2)得到快艇行驶过程y与t的函数关系式为:![]() ,
,
当快艇与乙港相距40 km时,快艇行驶了![]() ㎞,
㎞,
此时得到:![]() ,
,
解得![]() ,
,
由(1)知轮船的行驶速度是20km/h;
根据题意得到:当![]() ,轮船行驶了
,轮船行驶了![]() ,
,
故快艇和轮船相距![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120,△ABF为等边三角形;点E.F分别在菱形的边BC.CD上滑动,且点E.F不与点B.C.D重合,当点E.F分别在BC.CD上滑动时,求四边形ABCF的面积= ___________并求△CEF面积的最大值___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程
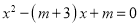
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若
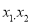 是原方程的两个实数根,且满足
是原方程的两个实数根,且满足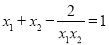 ,求m的值
,求m的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB∥CD,AB=CD,∠A=∠D.
(1)求证:四边形ABCD为矩形
(2)若点E是AB边上的中点,点F为AD边上一点,∠1=2∠2,CF=5,求AF+BC的值

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
新定义:任意两数a.b,按规定
 得到一个新数c,称所得新数c为数a.b的“快乐返校学习数”.
得到一个新数c,称所得新数c为数a.b的“快乐返校学习数”.(1)若a=1,b=2,求a,b的“快乐返校学习数”c.
(2)若
 ,b=
,b= ,且
,且 (0<m<1),求a,b的“快乐返校学习数”c.
(0<m<1),求a,b的“快乐返校学习数”c.(3)若a=2n+1,b=n-1,且a,b的“快乐返校学习数”c为正整数,求整数n的值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取前3格子中的任意两个数记作
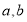 ,且
,且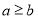 ,那么所有的
,那么所有的 的和可以通过计算
的和可以通过计算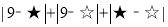 得到,其结果为_____,若
得到,其结果为_____,若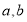 为前
为前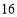 格子中的任意两个数,且
格子中的任意两个数,且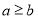 ,则所有的
,则所有的 的和为_____.
的和为_____.9
★
☆
x
﹣6
2
……
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
相关试题

