【题目】在平面直角坐标系中,B(2,0),A(6,6),M(0,6),P点为y轴上一动点。
(1)当P点在线段OM上运动时,试问是否存在一个点P使![]() =13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
=13,若存在,请求出P点耳朵坐标;若不存在,请说明理由.
(2)当点P在y的正半轴上运动时(不包括O,M),∠PAM,∠APB,∠PBO三者之间是否存在某种数量关系,如果有,请利用所学的知识找出并证明;如果没有,请说明理由。

参考答案:
【答案】(1)P(0,![]() );(2)当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.
);(2)当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.
【解析】
(1)设P(0,m).根据S△PAB=S梯形AMOB-S△APM-S△PBO,构建方程即可解决问题;
(2)分2种情形,分别画出图形,根据平行线的判定和性质解决问题即可.
(1)设P(0,m).
∵S△PAB=13,四边形AMOB是直角梯形,
∴![]() (6+2)6-
(6+2)6-![]() m2-
m2-![]() (6-m)6=13,
(6-m)6=13,
∴m=![]() ,
,
∴P(0,![]() ),
),
(2)①如图2-1中,当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;
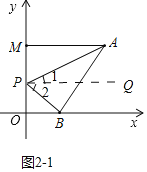
理由:作PQ∥AM,则PQ∥AM∥ON,
∴∠1=∠PAM,∠2=∠PBO,
∴∠1+∠2=∠PAM+∠PBO,
即∠APB=∠PAM+∠PBO,
∠APB+∠PBO=∠PAM;
②如图2-3中,当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.
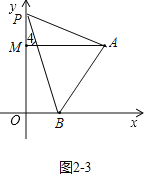
理由:∵AM∥OB,
∴∠4=∠PBO,
∵∠4=∠PAM+∠APB,
∴∠PBO=∠PAM+∠APB.
综合上述:当P在OM线段上,∠PAM+∠PBO=∠APB;当P在OM的延长线上,∠PAM+∠APB=∠PBO.
-
科目: 来源: 题型:
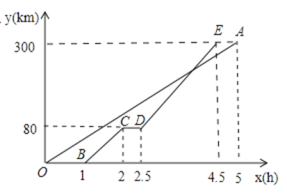
查看答案和解析>>【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地。如图,线段OA表示货车离甲地的距离
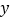 (km)与时间
(km)与时间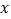 (h)之间的函数关系,折线BCDE变式轿车离甲地的距离
(h)之间的函数关系,折线BCDE变式轿车离甲地的距离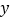 (km)与时间
(km)与时间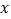 (h)之间的函数关系。根据图像,解答下列问题:
(h)之间的函数关系。根据图像,解答下列问题:(1)线段CD表示轿车在途中停留了 h.
(2)求线段DE对应的函数关系式(2.5≤x≤4.5).
(3)求轿车从甲地出发后经过多长时间追上货车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A8的坐标是( )

A.(﹣8,0)
B.(0,8)
C.(0,8 )
)
D.(0,16) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC﹣CD﹣DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y.如果y关于x的函数图象如图2所示,则△ABC的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和25,则△EDF的面积为( )

A. 35B. 25C. 15D. 12.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
相关试题

