【题目】如图,∠B、∠D的两边分别平行.
(1)在图1中, ∠B与∠D的数量关系是 ;
(2)在图2中, ∠B与∠D的数量关系是 ;
(3)用一句话归纳的结论为
(4)应用:若两个角的两边分别互相平行,其中一个角比另一个角的2倍小30°,求着两个角的度数.

参考答案:
【答案】(1)相等;(2)互补;(3)如果两个角的两边分别平行,那么这两个角相等或互补;(4)30°,30°或70°,110°.
【解析】
(1)由AB∥CD,BE∥DF,根据两直线平行,内错角相等,可得∠B=∠1,∠1=∠D,即可得∠B=∠D;
(2)由AB∥CD,BE∥DF,根据两直线平行,内错角相等,同旁内角互补,可得∠B=∠1,∠1+∠D=180°,即可得∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边分别互相平行,则这两个角相等或互补;
(4)由两个角的两边分别互相平行,可得这两个角的相等或互补,所以分两种情况讨论即可求得答案.
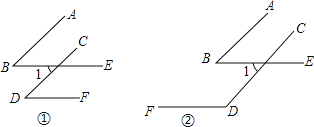
解:(1)∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1=∠D,
∴∠B=∠D.
故答案是∠B=∠D.
(2)∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1+∠D=180°,
∴∠B+∠D=180°.
故答案是∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补.
故答案为:若两个角的两边分别互相平行,则这两个角相等或互补.
(4)设一个角为x°,则另一个角的(2x-30)°,
若相等:x=2x-30,
解得:x=30,
则这两角分别为:30°,30°;
若互补,则x+2x-30=180,
解得:x=70,
则这两角分别为:70°,110°;
故答案为:30°,30°或70°,110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一条抛物线,三位学生分别说出了它的一些性质:
甲说:对称轴是直线x=2;
乙说:与x轴的两个交点距离为6;
丙说:顶点与x轴的交点围成的三角形面积等于9,请你写出满足
上述全部条件的一条抛物线的解析式: . -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
相关试题

