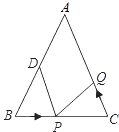
【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?
参考答案:
【答案】(1)全等,理由见解析;(2)![]() ,(3)
,(3)![]() .
.
【解析】试题分析:(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.
试题解析:(1)①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,  ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间![]() ,
,
∴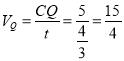 cm/s;
cm/s;
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]() .
.
∴点P共运动了![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm,
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠A:∠B:∠C=1:2:1,则∠D等于( )
A.0°
B.60°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x =
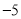 ,y =
,y = 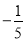 ,求
,求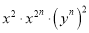 (n为正整数)的值;
(n为正整数)的值;(2)观察下列各式:32-12=8×1,52-32=8×2,72-52=8×3,…,探索以上式子的规律,试写出第n个等式,并运用所学的数学知识说明你所写式子的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
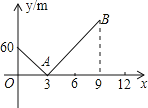
(1)弟弟步行的速度是 m/分,点B的坐标是 ;
(2)线段AB所表示的y与x的函数关系式是 ;
(3)试在图中补全点B以后的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不能能组成三角形的线段是( )
A. 5cm,3cm,6cmB. 3cm,4cm,5cmC. 2cm,4cm,6cmD. 5cm,6cm,9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条边的垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以每套80元的进价购进8套服装,并以90元左右的价格卖出.如果以90元为标准,超过标准的售价记为正数,不足标准的售价记为负数,出售价格记录如下:+2,﹣3,+5,+1,﹣2,﹣1,0,﹣5(单位:元).其它收支不计,当商店卖完这8套服装后( )
A. 盈利 B. 亏损 C. 不盈不亏 D. 盈亏不明
相关试题

