【题目】已知,∠AOD=160°,OB、OM、ON 是∠AOD内的射线
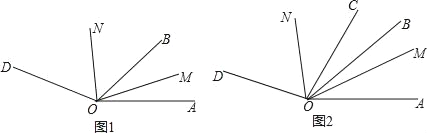
(1)如图1,若OM平分∠AOB,ON平分∠BOD,则∠MON= °
(2)如图2,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的大小;
(3)如图2,在(2)的条件下,当∠AOB=2t°时,∠AOM:∠DON=2:3,求t的值.
参考答案:
【答案】(1)80(2)70°(3)26
【解析】试题分析:(1)根据角平分线的性质,结合角的和差关系求解即可;
(2)根据题意,设∠AOB=x,则∠BOD=160°﹣x,然后根据角平分线的性质,结合角的和差关系求解即可;
(3)根据由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,然后根据比例关系列式求解即可.
试题解析:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD),
(∠AOB+∠BOD),
∵∠AOD=∠AOB+∠BOD=160°,
∴∠MON=![]() ×160°=80°;
×160°=80°;
故答案为:80;
(2)设∠AOB=x,则∠BOD=160°﹣x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=![]() ∠AOC=
∠AOC=![]() (x+20°),∠BON=
(x+20°),∠BON=![]() ∠BOD=
∠BOD=![]() (160°﹣x),
(160°﹣x),
∴∠MON=∠COM+∠BON﹣∠BOC=![]() (x+20°)+
(x+20°)+![]() (160°﹣x)﹣20°=70°;
(160°﹣x)﹣20°=70°;
(3)由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,
∴∠AOM=![]() ∠AOC=t°+10°,∠DON=
∠AOC=t°+10°,∠DON=![]() ∠BOD=80°﹣t°,
∠BOD=80°﹣t°,
∵∠AOM:∠DON=2:3,
∴![]() =
=![]() ,
,
解得:t=26.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=36°,∠A=∠B,则∠A=_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和是外角和的3倍,求此多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
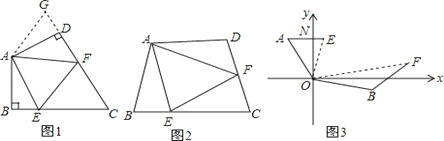
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=
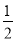 ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早上7点骑自行车从家出发,以每小时12千米的速度到距家4千米的学校上课,行至距学校1千米的地方时,自行车突然发生故障,小明只得改为步行前往学校,如果他想在7点30分之前赶到学校,那么他步行的速度至少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a﹣2)2+|b+3|=0,则ba的值是( )
A. ﹣9B. 9C. 8D. ﹣8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(a﹣1)x2﹣2x+1=0是一元二次方程,则a的取值范围是
相关试题

