【题目】如图,左面的几何体叫三棱柱,它有五个面,![]() 条棱,
条棱,![]() 个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
个顶点,中间和右边的几何体分别是四棱柱和五棱柱.

![]() 四棱柱有________个顶点,________条棱,________个面;
四棱柱有________个顶点,________条棱,________个面;
![]() 五棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
![]() 你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
![]() 棱柱有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
参考答案:
【答案】(1)![]() 六棱柱有
六棱柱有![]() 个顶点,
个顶点,![]() 条棱,
条棱,![]() 个面;七棱柱有
个面;七棱柱有![]() 个顶点,
个顶点,![]() 条棱,
条棱,![]() 个面;
个面;![]() 棱柱有
棱柱有![]() 个面,
个面,![]() 个顶点和
个顶点和![]() 条棱.
条棱.
【解析】
结合已知三棱柱、四棱柱和五棱柱的特点,可知n棱柱一定有(n+2)个面,2n个顶点和3n条棱.
(1)四棱柱有8个顶点,12条棱,6个面;
(2)五棱柱有10个顶点,15条棱,7个面;
(3)六棱柱有12个顶点,18条棱,8个面;
七棱柱有14个顶点,21条棱,9个面;
(4)n棱柱有(n+2)个面,2n个顶点和3n条棱。
-
科目: 来源: 题型:
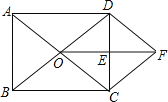
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一边长为
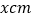 的正方形纸板的四个角各剪去一个边长为
的正方形纸板的四个角各剪去一个边长为 的小正方形,然后把它折成一个无盖纸盒.
的小正方形,然后把它折成一个无盖纸盒.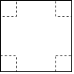
 求该纸盒的体积;
求该纸盒的体积; 求该纸盒的全面积(外表面积);
求该纸盒的全面积(外表面积); 为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时
为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时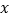 与
与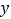 之间的倍数关系.(直接写出答案即可)
之间的倍数关系.(直接写出答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=∠B,∠4=65°,求证∠ACB=∠4.请填空完
成证明过程:
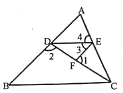
∵∠1+∠2=180°(______________)∠1+∠______=180°
∴∠2=∠DFE(___________________)
∴AB∥EF(____________________)
∴∠3=∠ADE(____________)
又∵∠3=∠B
∴∠ADE=∠_______
∴DE∥BC(____________)
∴∠ACB=∠4(_______________)
∴∠ACB=65°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中∠C=90°,放置边长分别为4、6、x的三个正方形,则x的值为( )
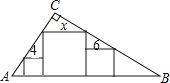
A.24
B.12
C.10
D.8
相关试题

