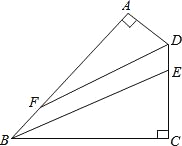
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.
(1)若∠ABC=50°,则∠ADC= °,∠AFD= °;
(2)BE与DF平行吗?试说明理由.
参考答案:
【答案】(1)120,30;(2)BE∥DF.见解析
【解析】试题分析:(1)根据四边形内角和为360°可计算出∠ADC=120°,再根据角平分线定义得到∠FDA=ADC=60°,然后利用互余可计算出∠AFD=30°;
(2)先根据BE平分∠ABC交CD于E得∠ABE=∠ABC=30°,而∠AFD=30°则∠ABE=∠AFD,于是可根据平行线的判定方法得到BE∥DF.
解:(1)∵∠A=∠C=90°,∠ABC=60°,
∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=120°,
∵DF平分∠ADC交AB于F,
∴∠FDA=ADC=60°,
∴∠AFD=90°﹣∠ADF=30°;
故答案为120,30;
(2)BE∥DF.理由如下:
∵BE平分∠ABC交CD于E,
∴∠ABE=∠ABC=×60°=30°,
∵∠AFD=30°;
∴∠ABE=∠AFD,
∴BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把a2﹣2a分解因式,正确的是( )
A. a(a﹣2) B. a(a+2) C. a(a2﹣2) D. a(2﹣a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于
 cm2?
cm2?
-
科目: 来源: 题型:
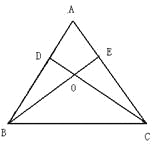
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三条边长分别是2,2x-3,6,则x的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三条高线的交点在三角形的一个顶点上,则此三角形是_____.
相关试题

