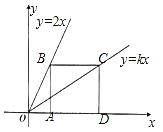
【题目】如图,点B、C分别在直线y=2x和y=kx上,点A、D是x轴上的两点,且四边形ABCD是正方形.
(1)若正方形ABCD的边长为2,则点B、C的坐标分别为 .
(2)若正方形ABCD的边长为a,求k的值.
参考答案:
【答案】(1)(1,2),(3,2)(2)![]()
【解析】
(1)根据正方形的边长,运用正方形的性质表示出点B、C的坐标;
(2)根据正方形的边长,运用正方形的性质表示出C点的坐标,再将C的坐标代入函数中,从而可求得k的值.
(1)∵正方形边长为2,
∴AB=2,
在直线y=2x中,当y=2时,x=1,
∴B(1,2),
∵OA=1,OD=1+2=3,
∴C(3,2),
故答案为:(1,2),(3,2);
(2)∵正方形边长为a,
∴AB=a,
在直线y=2x中,当y=a时,x=![]() ,
,
∴OA=![]() ,OD=
,OD=![]() ,
,
∴C(![]() ,a),
,a),
将C(![]() ,a)代入y=kx,得a=k×
,a)代入y=kx,得a=k×![]() ,
,
解得:k=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2﹣(﹣4)+3
(2)﹣32÷(﹣2)3
(3)(
 ﹣
﹣ +
+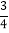 )×12
)×12(4)﹣13+[(﹣4)2﹣(1﹣32)×2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件的成本为10元,在试销阶段每件产品的日销售价x(元)与产品的日销售量y(件)之间的关系如下表:
X(元)
15
20
25
…
Y(件)
25
20
15
…
(1)观察与猜想y与x的函数关系,并说明理由.
(2)求日销售价定为30元时每日的销售利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论:
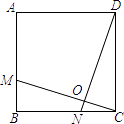
①DN⊥MC;②DN垂直平分MC;③sin∠OCD=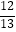 ;④S△ODC=S四边形BMON中,
;④S△ODC=S四边形BMON中,
正确的有(填写序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解不等式
(1)计算:(3﹣π)0+2tan60°+(﹣1)2015﹣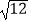 .
.
(2)解不等式组: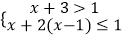 ,并把它的解在数轴上表示出来.
,并把它的解在数轴上表示出来. 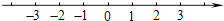
-
科目: 来源: 题型:
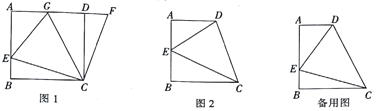
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.

相关试题

