【题目】(本题满分12分)如图,在数轴上点A、B、C表示的数分别为-2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)则AB=______,BC=______,AC=______;
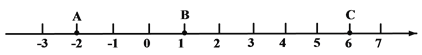
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:BC-AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
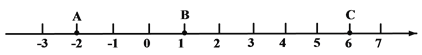
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:随着运动时间t的变化,AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.
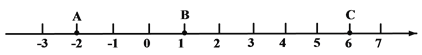
参考答案:
【答案】(1)AB=3,BC=5,AC=8;(2)BC-AB的值不会随着时间t的变化而改变,BC-AB=2 ;
(3)当t≤1时,AB+BC=AC;当1<t≤2时,BC+AC=AB;当t>2时,AB+AC=BC.
【解析】试题分析:(1)根据点A、B、C在数轴上的位置,写出AB、BC、AC的长度;
(2)求出BC和AB的值,然后求出BC-AB的值,判断即可;
(3)分别表示出AB、BC、AC的长度,然后分情况讨论得出之间的关系.
试题解析:(1)由图可得,AB=3,BC=5,AC=8,
(2)BC-AB=(5t-2t+5)-(t+2t+3)=2,
故BC-AB的值不会随着时间t的变化而改变;
(3)由题意得,AB=t+3,
BC=5-5t(t≤1时)或BC=5t-5(t>1时),
AC=8-4t(t≤2时)或AC=4t-8(t>2时),
当t≤1时,AB+BC=(t+3)+(5-5t)=8-4t=AC,
当1<t≤2时,BC+AC=(5t-5)+(8-4t)=t+3=AB,
当t>2时,AB+AC=(t+3)+(4t-8)=5t-5=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式23a2b3的系数和次数分別是
A. 2,8 B. 8,5 C. 2,8 D. 2,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】遵义市是国家级红色旅游城市,每年都吸引众多海内外游客前来观光、旅游.据有关部门统计报道:2012年全市共接待游客3354万人次.将3354万用科学记数法表示为( )
A.3.354×106
B.3.354×107
C.3.354×108
D.33.54×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚想买双好的运动鞋,于是他上网查找有关资料,得到下表:
颜色
价格(元)
备注
甲
红、白、蓝、灰
450
不宜在雨中穿
乙
淡黄、浅绿、白、黑
700
有很好的防水性
丙
灰、白蓝相间
350
较为防水
丁
浅绿、淡黄、白蓝相间
500
防水性很好
他想买一双价格在300~600元之间,白蓝相间、浅绿或淡黄色,并且防水性能很好的运动鞋,那么他应选( )
A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2
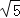 DE,求tan∠ABD的值.
DE,求tan∠ABD的值.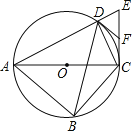
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条不平行的直线被第三条直线所截,下列说法可能成立的是( )
A.同位角 相等
B.内错角相等
C.同旁内角相等
D.同旁内角互补 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3﹣x= .
相关试题

