【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)ΔABE与ΔADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求FD的长.

参考答案:
【答案】(1)、相似,证明过程见解析;(2)、FD=7.2
【解析】
试题分析:(1)、首先根据矩形和DF⊥AE可得∠B=∠AFD,根据AD∥BC可得∠DAF=∠AEB,从而得出三角形相似;(2)、首先根据Rt△ABE的勾股定理求出AE的长度,然后根据三角形相似得出DF的长度.
试题解析:(1)、∵ABCD为矩形 ∴∠BAD=∠B=90° ∵DF⊥AE ∴∠AFD=90°
∵AD∥BC ∴∠DAF=∠AEB 在△ABE和△AFD中 ∠B=∠AFD,∠DAF=∠AEB ∴△ABE∽△ADF
(2)、∵AB=6,BE=8,∠B=90° ∴AE=10 ∵△ABE∽△ADF ∴![]()
∴![]() ∴DF=7.2
∴DF=7.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是最小的正整数,c是绝对值最小的数,则(a+c)÷b=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录了七(1)班一个组学生的体重情况,假设平均体重是50 kg,超出记为正,不足记为负.
姓名
小明
小丁
小丽
小文
小天
小乐
体重与平均
体重的差值/kg
-5
+3
-7
+4
+6
-1
(1)谁最重?谁最轻?
(2)最重的同学比最轻的同学重多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程没有实数根的是( )
A.x2+2x+1=0
B.x2+x+2=0
C.x2﹣1=0
D.x2﹣2x﹣1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知二次函数图象的顶点坐标为C(1,0),直线
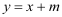 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴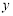 上.
上.(1)、求
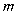 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;(2)、P为线段AB上的一个动点(点P与A、B不重合),过P作
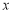 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为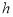 ,点P的横坐标为
,点P的横坐标为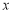 ,求
,求 与
与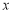 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量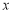 的取值范围;
的取值范围;(3)、D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a4=a12B.a5÷a3=a2C.(3a4)2=6a8D.(﹣a)5a=a6
相关试题

