搜索
【题目】如图，已知直角三角形ABC中，∠ACB=90°，E为AB上一点，且CE=EB，ED⊥CB于D，则下列结论中不一定成立的是（ ）
A.AE=BEB.CE=
ABC.∠CEB=2∠AD.AC=AB
参考答案：
【答案】D
【解析】
根据线段垂直平分线的性质和等腰三角形的性质及三角形的内角和即可推得．
∵CE=EB，∴∠B=∠BCE．
∵∠ACB=90°，
∴∠ACE+∠BCE=90°，∠A+∠B=90°．
∴∠A=∠ACE．
∴AE=CE=EB．
故选项A、B都正确；
∵∠ACB=90°，ED⊥CB，
∴AC∥ED．
则∠A=∠DEB，∠CED=∠ACE．
又∠A=∠ACE，
∴∠CEB=2∠A．
故选项C正确；
当∠B=30°或∠A=60°时，选项D才成立．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y=
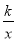的图象上，则k的值为__．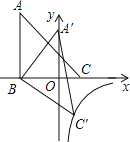
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数按要求分类
＋8.3，－4，－0.8，－
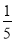，0，π，90，－|－24|，15％，
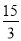中，负数有______________________________，
分数有______________________________．
整数有______________________________．
有理数有______________________________．
-
科目： 来源： 题型：
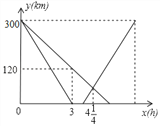
查看答案和解析>>【题目】某客运公司的特快巴士与普通巴士同时从甲地出发，以各自的速度匀速向乙地行驶，普通巴士到达乙地后停止，特快巴士到达乙地停留45分钟后，按原路以另一速度匀速返回甲地，已知两辆巴士分别距乙地的路程y（千米）与行驶时间x（小时）之间的函数图象如图所示．求普通巴士到达乙地时，特快巴士与甲地之间的距离为_____千米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有
、
、
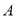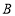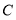三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）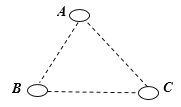
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ΔABC中，AB＝AC，AB的垂直平分线交AC于P点．
（1）若∠A＝35°，则∠BPC＝_____；
（2）若AB＝5 cm，BC＝3 cm，则ΔPBC的周长＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料:
问题：如图1，在平行四边形ABCD中,E是AD上一点，AE=AB，∠EAB=60°，过点E作直线EF，在EF上取一点G.使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
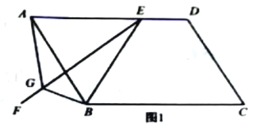
小明同学的思路是:作∠CAM=∠EAB交CE于点H，构造全等三角形，经过推理解决问题.
参考小明同学的思路，探究并解决下列问题:
(1)完成上面问题中的证明；
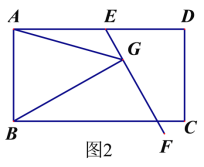
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变(如图2),请探究线段EC、AG、BG之间的数量关系,并证明你的结论.
解:线段EG、AG、BG之间的数量关系为___________________________________________________.证明:
相关试题
