【题目】如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
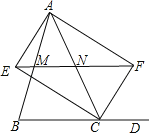
(1)四边形AECF是矩形;
(2)MN=![]() BC.
BC.
参考答案:
【答案】见解析
【解析】
试题分析:(1)由角平分线的定义和邻补角定义得出∠ECF=90°,由AE⊥CE,AF⊥CF,得出∠AEC=∠AFC=90°,即可得出四边形AECF是矩形;
(2)由矩形的性质得出EN=FN,AN=CN=![]() AC,由直角三角形斜边上的中线性质得出CN=
AC,由直角三角形斜边上的中线性质得出CN=![]() EF=EN,由等腰三角形的性质得出∠NEC=∠ACE=∠BCE,证出EN∥BC,得出△AMN∽△ABC,由相似三角形的对应边成比例即可得出结论.
EF=EN,由等腰三角形的性质得出∠NEC=∠ACE=∠BCE,证出EN∥BC,得出△AMN∽△ABC,由相似三角形的对应边成比例即可得出结论.
证明:(1)∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠BCE=![]() ∠ACB,∠ACF=
∠ACB,∠ACF=![]() ∠ACD,
∠ACD,
∵∠ACB+∠ACD=180°,
∴∠ACE+∠ACF=90°,
即∠ECF=90°,
又∵AE⊥CE,AF⊥CF,
∴∠AEC=∠AFC=90°,
∴四边形AECF是矩形;
(2)∵四边形AECF是矩形,
∴EN=FN,AN=CN=![]() AC,
AC,
∴CN=![]() EF=EN,
EF=EN,
∴∠NEC=∠ACE=∠BCE,
∴EN∥BC,
∴△AMN∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴MN=![]() BC.
BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+mx+4能用完全平方公式分解因式,则m的值可以是( )
A. 4 B. -4 C. ±2 D. ±4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
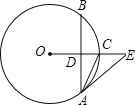
(1)求证:直线AE是⊙O的切线;
(2)若AB=8,sin∠E=
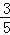 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解xy-4y的正确结果是( )
A. y(x+4)(x-4) B. y(x-4 ) C. y(x-2) D. y(x+2)(x-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
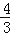 x+4分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
x+4分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.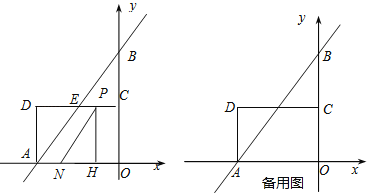
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作PH⊥OA,垂足为H,连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1,求t的值;
②点Q是点B关于点A的对称点,问BP+PH+HQ是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A. y轴对称 B. x轴对称 C. 原点对称 D. 直线y=x对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年10月18日,TCL2015长沙国际马拉松赛正式开赛,来自国内外的1.5万余名选手在长沙这座美丽的城市中奔跑.马拉松长跑是国际上非常普及的长跑比赛项目,全程距离约为42千米,将数据42千米用科学记数法表示为( )
A.42×103米 B.0.42×105米 C.4.2×104米 D.4.2×105米
相关试题

