【题目】如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
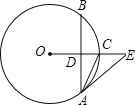
(1)求证:直线AE是⊙O的切线;
(2)若AB=8,sin∠E=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)见解析;(2)5
【解析】
试题分析:(1)首先得出∠OCA+∠CAD=90°,进而求出∠EAC+∠OAC=90°,即可得出答案.
(2)作CF⊥AE于F,根据角平分线的性质和三角函数求得AE=![]() ,DE=
,DE=![]() ,进一步求得CF=CD=2,然后根据勾股定理列出关于r的方程,解方程即可求得.
,进一步求得CF=CD=2,然后根据勾股定理列出关于r的方程,解方程即可求得.
(1)证明:连接OA,
∵OE垂直于弦AB,
∴∠OCA+∠CAD=90°,
∵CO=OA,
∴∠OCA=∠OAC,
∵∠EAC=∠CAB,
∴∠EAC+∠OAC=90°,
∴OA⊥AE,
即直线AE是⊙O的切线.
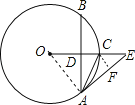
(2)作CF⊥AE于F,
∵∠EAC=∠CAB,
∴CF=CD,
∵AB=8,
∴AD=4,
∵sin∠E=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴AE=![]() ,DE=
,DE=![]() ,
,
∴CF=2,
∴CD=2,
设⊙O的半径r,
在RT△AOD中,OA2=OD2+AD2,即r2=(r﹣2)2+42,
解得r=5.
∴⊙O的半径为5.
-
科目: 来源: 题型:
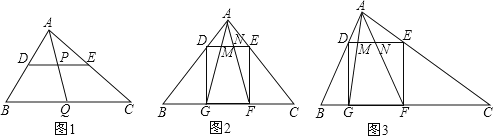
查看答案和解析>>【题目】(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:
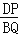 =
=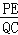 ;
;(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DMEN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接元旦小长假的购物高峰,黄兴南路步行街某运动品牌专卖店购进甲、乙两种服装,现此商店同时卖出甲、乙两种服装各一件,每件售价都为240元,其中一件赚了20%,另一件亏了20%,那么这个商店卖出这两件服装总体的盈亏情况是( )
A.赚了12元 B.亏了12元 C.赚了20元 D.亏了20元
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+mx+4能用完全平方公式分解因式,则m的值可以是( )
A. 4 B. -4 C. ±2 D. ±4
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解xy-4y的正确结果是( )
A. y(x+4)(x-4) B. y(x-4 ) C. y(x-2) D. y(x+2)(x-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
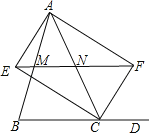
(1)四边形AECF是矩形;
(2)MN=
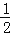 BC.
BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
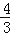 x+4分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
x+4分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.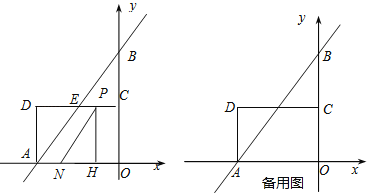
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作PH⊥OA,垂足为H,连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1,求t的值;
②点Q是点B关于点A的对称点,问BP+PH+HQ是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
相关试题

