搜索
【题目】观察下列等式：21=2，22=4，23=8，24=16，25=32，26=64，…，根据这个规律，则21+22+23+…+22019的末尾数字是______．
参考答案：
【答案】4
【解析】
根据已知算式得出规律，求出504×（2+4+8+6）+2+4+8的结果，即可得出答案．
∵21=2，22=4，23=8，24=16，25=32；26=64，
2019÷4=504…3，
∴504×(2+4+8+6)+2+4+8=10094，
∴21+22+23+24+25+……+22019的末尾数字为4，
故答案为：4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）先化简，再求值: (a+1)2-(3a2+a)÷a，其中a=-3.
（2）已知x+y=3，xy=-2. 求(x-1)(y-1)的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a、b、c的大小关系为：c＜b＜0＜a，则下面的判断正确的是（ ）
A.abc＜0
B.a﹣b＞0
C.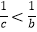
D.c﹣a＞0 -
科目： 来源： 题型：
查看答案和解析>>【题目】在二次函数y=x2﹣2x﹣3中，当0≤x≤3时，y的最大值和最小值分别是（ ）
A.0，﹣4
B.0，﹣3
C.﹣3，﹣4
D.0，0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的运算程序中，若开始输入的x值为12，我们发现第1次输出的结果为6，第2次输出的结果为3，…第2017次输出的结果为（ ）
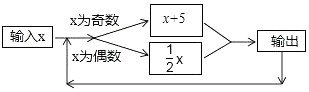
A.3
B.6
C.4
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形的三边a，b，c能满足a2+b2=nc2（n为正整数），那么这个三角形叫做“n阶三角形”．如三边分别为1、2、
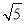的三角形满足12+22=1×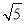（）2，所以它是1阶三角形，但同时也满足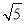（）2+22=9×12，所以它也是9阶三角形．显然，等边三角形是2阶三角形，但2阶三角形不一定是等边三角形．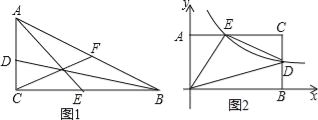
（1）在我们熟知的三角形中，何种三角形一定是3阶三角形？
（2）若三边分别是a，b，c（a＜b＜c）的直角三角形是一个2阶三角形，求a：b：c．
（3）如图1，直角△ABC是2阶三角形，AC＜BC＜AB，三条中线BD、AE、CF所构成的三角形是何种三角形？四位同学作了猜想：
A同学：是2阶三角形但不是直角三角形；
B同学：是直角三角形但不是2阶三角形；
C同学：既是2阶三角形又是直角三角形；
D同学：既不是2阶三角形也不是直角三角形．
请你判断哪位同学猜想正确，并证明你的判断．
（4）如图2，矩形OACB中，O为坐标原点，A在y轴上，B在x轴上，C点坐标是（2，1），反比例函数y=
（k＞0）的图象与直线AC、直线BC交于点E、D，若△ODE是5阶三角形，直接写出所有可能的k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算3ab25a2b的结果是（ ）
A. 8a2b2 B. 8a3b3 C. 15a3b3 D. 15a2b2
相关试题
