【题目】关于x的一元二次方程x2-(k+3)x+2k+2=0.
(1)若k=0,求方程的解;
(2)求证:无论k取任何实数时,方程总有两个实数根.
参考答案:
【答案】(1)x=1或x=2;(2)见解析.
【解析】
(1)直接代入k=0,求解方程;
(2) 证明无论k取任何实数时, △≥0,即方程总有两个实数根.
解:(1)当k=0时,方程为x2﹣3x+2=0,
则(x﹣1)(x﹣2)=0,
所以x﹣1=0或x﹣2=0,
解得:x=1或x=2;
(2)∵△=[﹣(k+3)]2﹣4×1×(2k+2)
=k2+6k+9﹣8k﹣8
=k2﹣2k+1
=(k﹣1)2≥0,
∴方程总有2个实数根.
-
科目: 来源: 题型:
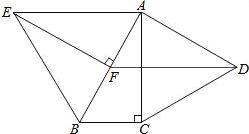
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】人往路灯下行走的影子变化情况是( )
A.长短长 B.短长短 C.长长短 D.短短长
-
科目: 来源: 题型:
查看答案和解析>>【题目】列等式表示:比a的3倍大4的数等于a的5倍,得 ________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是( )
A. 正方形 B. 长方形 C. 线段 D. 梯形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为1cm,若点P到圆心O的距离为0.5 cm,则点P与⊙O的位置关系是( )
A. 点P在⊙O外 B. 点P在⊙O上 C. 点P在⊙O内 D. 无法确定
相关试题

