【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点B′处.
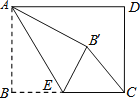
(1)矩形ABCD的面积= ;
(2)当△CEB′为直角三角形时,BE= .
参考答案:
【答案】(1)48;(2)3或6.
【解析】
试题分析:(1)直接利用矩形的面积求出答案;
(2)当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时四边形ABEB′为正方形.
解:(1)∵在矩形ABCD中,AB=6,BC=8,
∴矩形ABCD的面积=6×8=48;
故答案为:48;
(2)当△CEB′为直角三角形时,有两种情况:

①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,
∴EB=EB′,AB=AB′=6,
∴CB′=10﹣6=4,
设BE=x,则EB′=x,CE=8﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴BE=3;
②当点B′落在AD边上时,如答图2所示.

此时ABEB′为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故答案为:3或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个有理数的和为正数,那么这两个数一定( )
A. 都是正数 B. 至少有一个正数
C. 有一个是0 D. 绝对值不相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能使两个直角三角形全等的条件是( )
A. 斜边、直角边对应相等
B. 两直角边对应相等
C. 一锐角和斜边对应相等
D. 两锐角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店有两套进价不同的羽绒服都卖了640元,其中一个盈利60%,另一个亏损20% ,在这次买卖中,这家商店( )
A. 赔了24元 B. 赚了32元 C. 赔了64元 D. 赚了80元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上的一点,且AC平分∠PAE,过C作CD⊥PA于点D.
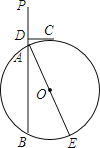
(1)求证:CD为⊙O的切线.
(2)若DC+DA=6,AE=26,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年7月30日,中国人民解放军将以一场气势磅礴的沙场阅兵庆祝90岁生日,在朱日和约有12000兵力接受了检阅,12000用科学记数法表示为______________.
相关试题

