【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒). 
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.
参考答案:
【答案】
(1)解:∠MOA=2t
(2)解:如图,
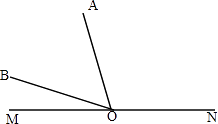
根据题意知:∠AOM=2t,∠BON=4t,
当∠AOB第二次达到60°时,∠AOM+∠BON﹣∠MON=60°,
即2t+4t﹣180=60,解得:t=40,
故t=40秒时,∠AOB第二次达到60°
(3)解:射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有以下三种情况:
①OB平分∠AOM时,∵ ![]() ∠AOM=∠BOM,
∠AOM=∠BOM,
∴t=180﹣4t,或t=4t﹣180,
解得:t=36或t=60;
②OB平分∠MON时,∵∠BOM= ![]() ∠MON,即∠BOM=90°,
∠MON,即∠BOM=90°,
∴4t=90,或4t﹣180=90,
解得:t=22.5,或t=67.5;
③OB平分∠AON时,∵∠BON= ![]() ∠AON,
∠AON,
∴4t= ![]() (180﹣2t),或180﹣(4t﹣180)=
(180﹣2t),或180﹣(4t﹣180)= ![]() (180﹣2t),
(180﹣2t),
解得:t=18或t=90(不符合题意,舍去);
综上,当t的值分别为18、22.5、36、60、67.5秒时,射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线
【解析】(1)∠AOM的度数等于OA旋转速度乘以旋转时间;(2)当∠AOB第二次达到60°时,射线OB在OA的左侧,根据∠AOM+∠BON﹣∠MON=60°列方程求解可得;(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有三种情况:①OB两次平分∠AOM时,根据 ![]() ∠AOM=∠BOM,列方程求解,
∠AOM=∠BOM,列方程求解,
②OB两次平分∠MON时,根据∠BOM= ![]() ∠MON,列方程求解,
∠MON,列方程求解,
③OB平分∠AON时,根据∠BON= ![]() ∠AON,列方程求解.
∠AON,列方程求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,且∠AOC=∠COB﹣40°,求∠BOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C、D、E在线段AB上,且满足AC=CD=DB,点E是线段DB的中点,若线段CE=6cm,求线段AB的长.
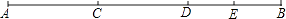
-
科目: 来源: 题型:
查看答案和解析>>【题目】某两位数,十位上的数字为a,个位上的数字为b,则这个两位数可表示为 ( )
A. ab B. a+b C. 10a+b D. 10b+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数据为边长,能构成三角形的是:
A. 4,4,8 B. 2,4,7 C. 4,8,8 D. 2,2,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则这组数据的中位数和众数分别是( )
阅读量(单位:本/周)
0
1
2
3
人数(单位:人)
1
4
6
4
A.1,2B.2,2C.4,6D.6,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和与它的外角和的比为5:2,则这个多边形的边数为:
A. 8 B. 7 C. 6 D. 5
相关试题

