【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.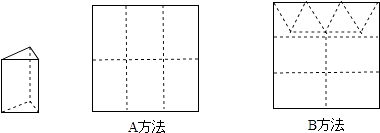
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
参考答案:
【答案】
(1)解:∵裁剪时x张用A方法,
∴裁剪时(19﹣x)张用B方法.
∴侧面的个数为:6x+4(19﹣x)=(2x+76)个,
底面的个数为:5(19﹣x)=(95﹣5x)个
(2)解:由题意,得
![]() ,
,
解得:x=7,
经检验,x=7是原分式方程的解,
∴盒子的个数为: ![]() =30.
=30.
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子
【解析】(1)由x张用A方法,就有(19﹣x)张用B方法,就可以分别表示出侧面个数和底面个数;(2)由侧面个数和底面个数比为3:2建立方程求出x的值,求出侧面的总数就可以求出结论.
【考点精析】关于本题考查的分式方程的应用,需要了解列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-b)4·(-b)3·(-b)5=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
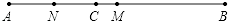
(1)若AB=8cm,AC=3.2cm,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x3)2的结果是( )
A.x5
B.x6
C.x8
D.x9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4的图象经过点(m,8),则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式5xm+2+3是关于x的一次二项式,则m= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】10m+1×10n-1=__________,-64×(-6)5=__________.
相关试题

