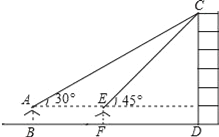
【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
参考答案:
【答案】这栋建筑物CD的高度约为29m
【解析】试题分析:延长AE交CD于点G,设CG=xm,在直角△CGE中利用x表示出EG,然后在直角△ACG中,利用x表示出AG,根据AE=AG-EG即可列方程求得x的值,进而求出CD的长.
试题解析:
解:延长AE交CD于点G.

设CG=xm,
在直角△CGE中,∠CEG=45°,则EG=CG=xm.
在直角△ACG中,AG= ![]() .
.
∵AG-EG=AE, ∴![]() ,
,
解得: ![]() (m).
(m).
则CD=27.32+1.5=28.82≈29(m).
答:这栋建筑物CD的高度约为29m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2﹣2mx+4是一个完全平方式,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题的个数是( )
①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
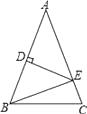
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=cm.
-
科目: 来源: 题型:
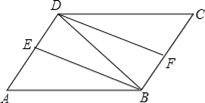
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:△ABE≌△CDF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(2a﹣6,a+1),若点P在坐标轴上,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
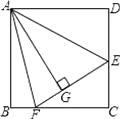
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
相关试题

