【题目】如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
(1)PA与PB相等吗?请说明理由;
(2)若![]() ,求圆环的面积.
,求圆环的面积.

参考答案:
【答案】(1)相等,证明见解析;(2)圆环的面积为![]()
【解析】试题分析:(1)PA=PB,连接OP,在大圆中利用垂径定理即可证明,
(2)连接OA,根据切线的性质和勾股定理可得:OA2﹣OP2=![]() AB2,写出环形的面积表达式,把数值代入即可.
AB2,写出环形的面积表达式,把数值代入即可.
试题解析:(1)PA=PB,理由如下:
连接OP,
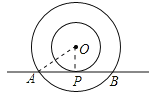
∵大圆的弦AB切小圆于点P,
∴OP⊥AB,
∴PA=PB,
(2)接OA,
∵大圆中长为8的弦AB与小圆相切,
∴OP⊥AB,AP=4,
∴OA2﹣OP2=16,
∴πOA2﹣πOP2=(OA2﹣OP2)π,
∴圆环的面积=16π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量y(升)与行驶时间t(小时)之间的关系用如图的线段AB表示.根据图象求得y与t的关系式为
 ,这里的常数“-7.5”,“25”表示的实际意义分别是( )
,这里的常数“-7.5”,“25”表示的实际意义分别是( )
A.“-7.5”表示每小时耗油7.5升,“25”表示到达乙地时油箱剩余油25升
B.“-7.5”表示每小时耗油7.5升,“25”表示出发时油箱原有油25升
C.“-7.5”表示每小时耗油7.5升,“25”表示每小时行驶25千米
D.“-7.5”表示每小时行驶7.5千米,“25”表示甲乙两地的距离为25千米 -
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a﹣3,a+4)在x轴上,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,
 ,
,  .
.(1)求∠BOC的度数;
(2)求∠EDF的度数.
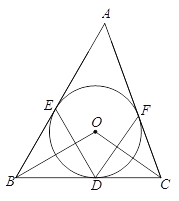
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为
 ,点D的坐标为
,点D的坐标为 .
.(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】七边形的七个内角与它的一个外角的度数和可能是( )
A. 800° B. 900° C. 1000° D. 1100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
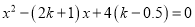
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为
 ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
相关试题

