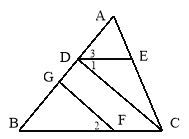
【题目】如图,∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的位置关系,并说明理由.
参考答案:
【答案】垂直;理由见解析
【解析】
试题分析:根据∠3=∠B得出ED∥BC,根据FG⊥AB得出∠AGF=90°,根据外角的性质得出∠AGF=∠B+∠2,结合∠ADC=∠1+∠3,∠1=∠2,∠3=∠B从而得出∠ADC=∠AGF=90°,从而得到垂直.
试题解析:猜想CD⊥AB.
理由如下: ∵∠3=∠B(已知),∴ED∥BC(同位角相等,两直线平行).
∵FG⊥AB(已知),∴∠AGF=90°(垂直定义).
∵∠AGF是△BFG的一个外角, ∴∠AGF=∠B+∠2(三角形的一个外角等于和它不相邻的两个内角的和).
∵∠ADC=∠1+∠3,而∠1=∠2,∠3=∠B, ∴∠ADC=∠AGF=90°(等量代换).
∴CD⊥AB(垂直定义).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)

(2)-4a(2
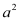 +3a-1)
+3a-1) (3)

(4)
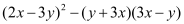 .
. (5)(2x-y+1)(2x+y-1)
(6) 用简便方法计算:
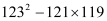
(7)先化简,再求值:(2x+3)(2x-3)-2x(x-1)-2(x-1)2,其中x=-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E, CF∥AD.
(1)如图①,∠B=30°,∠ACB=70°,则∠CFE=_________;
(2)若(1)中的∠B=
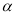 ,∠ACB=
,∠ACB= ,则∠CFE=_________;(用
,则∠CFE=_________;(用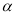 、
、 表示)
表示)(3)如图②,(2)中的结论还成立么?请说明理由。
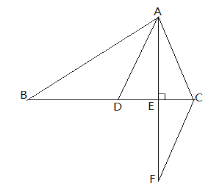
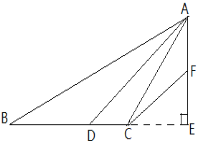
图① 图②
-
科目: 来源: 题型:
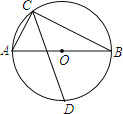
查看答案和解析>>【题目】如图,⊙O的直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,则CD长是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的顶角y与底角x之间是函数关系吗?_________(是或不是中选择)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①在同一直线上的四点A,B,C,D任意两点相连的线段,只能表示4条不同的线段;②经过两点有一条直线,并且只有一条直线;③一个锐角的补角一定大于它本身.正确的是( )
A. ②③ B. ③ C. ①② D. ①
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的各组线段中,能组成一个三角形的是
A. 3,5,10 B. 10,4,6 C. 4,6,9 D. 3,1,1
相关试题

