【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
参考答案:
【答案】(1)9.5,10;(2)1;(3)乙
【解析】
试题分析:(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:![]() (10×4+8×2+7+9×3)=9,
(10×4+8×2+7+9×3)=9,
则方差是:![]() [4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为( )
A.y=2(x﹣3)2+2
B.y=2(x+3)2+2
C.y=2(x+3)2﹣2
D.y=2(x﹣3)2﹣2 -
科目: 来源: 题型:
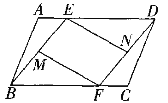
查看答案和解析>>【题目】如图,在□ABCD中,AE=CF,M、N分别是BE、DF的中点,试说明四边形MFNE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有3个红球和1个白球,这些球除颜色外都相同.
(1)从中随机摸出1个球,记录颜色后放回,搅匀,再摸出1个球.摸出的两个球中,1个为红球,1个为白球的概率为 ;
(2)从中随机摸出1个球,记录颜色后不放回,再摸出1个球.求摸出的两个球中,1个为红球,1个为白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.

(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
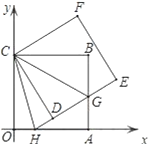
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程;3x-2(x-1)=4
相关试题

