搜索
【题目】如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处，若AB=6cm，AC=10cm，则四边形AECF的面积为cm2.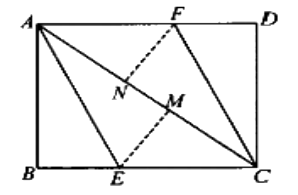
参考答案：
【答案】30
【解析】解：在矩形ABCD中，AB=6，AC=10，∴BC= 
8cm.
由折叠的性质可得AM=AB=6，EM=BE，∠AME=∠B=90°，则CM=10-6=4cm.
设EM=BE=x，则CE=8-x，
由勾股定理得 
得 
，解得x=3,即EM=3.
同理可得FN⊥AC，EF=3，
则四边形AECF的面积为 
=30cm2.
所以答案是30.
【考点精析】掌握翻折变换（折叠问题）是解答本题的根本，需要知道折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABN中，∠B =90°，点M是AB上的动点（不与A,B两点重合），点C是BN延长线上的动点（不与点N重合），且AM=BC，CN=BM，连接CM与AN交于点P.
（1）在图1中依题意补全图形;
（2）小伟通过观察、实验，提出猜想:在点M，N运动的过程中，始终有∠APM=45°.小伟把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的一种思路:
要想解决这个问题，首先应想办法移动部分等线段构造全等三角形，证明线段相等，再构造平行四边形，证明线段相等，进而证明等腰直角三角形，出现45°的角，再通过平行四边形对边平行的性质，证明∠APM=45°.
他们的一种作法是：过点M在AB下方作MD
AB于点M,并且使MD=CN.通过证明△AMD
△CBM,得到AD=CM,再连接DN，证明四边形CMDN是平行四边形，得到DN=CM，进而证明△ADN是等腰直角三角形，得到∠DNA=45°.又由四边形CMDN是平行四边形，推得∠APM=45°.使问题得以解决.请你参考上面同学的思路，用另一种方法证明∠APM=45°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数y＝－x2＋2x，有下列四个结论：①它的对称轴是直线x＝1；②设y1＝－
＋2x1，y2＝－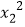
＋2x2，则当x2＞x1时，有y2＞y1；③它的图象与x轴的两个交点是(0，0)和(2，0)；④当0＜x＜2时，y＞0.其中正确结论的个数为( )A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究归纳题：
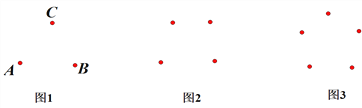
(1)试验分析：
如图1，经过A点与B、C两点分别作直线，可以作____________条；同样，经过B点与A、C两点分别作直线，可以作______________条；经过C点与A、B两点分别作直线，可以作___________条.
通过以上分析和总结，图1共有___________条直线.
（2）拓展延伸：
运用（1）的分析方法，可得：
图2共有_____________条直线；
图3共有_____________条直线；
(3)探索归纳：
如果平面上有n(n≥3)个点，且每3个点均不在同一直线上，经过其中两点共有________条直线．(用含n的式子表示)
(4)解决问题：
中职篮（CBA）2017——2018赛季作出重大改革，比赛队伍数扩充为20支，截止2017年12月21日赛程过半，即每两队之间都赛了一场，请你帮助计算一下一共进行了多少场比赛？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某景区在“五一”小长假期间，每天接待的旅客人数统计如下表．
日期
5月1日
5月2日
5月3日
5月4日
5月5日
人数（万人）
1.2
2
2.5
2
1.1
表中表示人数的一组数据中，众数和中位数分别为（ ）
A.2.5万，2万B.2.5万，2.5万C.2万，2.5万D.2万，2万
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A1，A2在射线OA上，B1在射线OB上，依次作A2B2∥A1B1，A3B2∥A2B1，A3B3∥A2B2，A4B3∥A3B2，…. 若
和
的面积分别为1、9，则
的面积是_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】0．25°等于（ ）分．
A.60
B.15
C.90
D.360
相关试题
