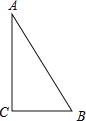
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
参考答案:
【答案】(1)18;(2)3;(3)t=6s或13s或12s或 10.8s 时△BCP为等腰三角形;(4)t为4或12秒时,直线PQ把△ABC的周长分成相等的两部分
【解析】试题分析:(1)、根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长.(2)、因为AB与CB,由勾股定理得AC="4" 因为AB为5cm,所以必须使AC=CB,或CB=AB,所以必须使AC或AB等于3,有两种情况,△BCP为等腰三角形.(3)、分类讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t﹣3,t+2t﹣3=6;当P点在AB上,Q在AC上,则AC=t﹣4,AQ=2t﹣8,t﹣4+2t﹣8=6.
试题解析:(1)、如图1,由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2, ∵∠C=90°, ∴PB=![]() =
=![]() ,
,
∴△ABP的周长为:AP+PB+AB=2+5+![]() =7
=7![]() .
.
(2)、①如图2,若P在边AC上时,BC=CP=3cm,
此时用的时间为3s,△BCP为等腰三角形;
②若P在AB边上时,有三种情况: i)如图3,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,
所以用的时间为6s,△BCP为等腰三角形;
ii)如图4,若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm, 作CD⊥AB于点D,
在Rt△PCD中,PD=![]() =
=![]() =1.8, 所以BP=2PD=3.6cm,
=1.8, 所以BP=2PD=3.6cm,
所以P运动的路程为9﹣3.6=5.4cm, 则用的时间为5.4s,△BCP为等腰三角形;
ⅲ)如图5,若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形
(3)、如图6,当P点在AC上,Q在AB上,则PC=t,BQ=2t﹣3,
∵直线PQ把△ABC的周长分成相等的两部分, ∴t+2t﹣3=3, ∴t=2;
如图7,当P点在AB上,Q在AC上,则AP=t﹣4,AQ=2t﹣8,
∵直线PQ把△ABC的周长分成相等的两部分, ∴t﹣4+2t﹣8=6, ∴t=6,
∴当t为2或6秒时,直线PQ把△ABC的周长分成相等的两部分.


-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣0.5的绝对值是( )
A.0.5
B.﹣0.5
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥d
B.b⊥d
C.a⊥d
D.b∥c -
科目: 来源: 题型:
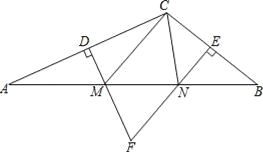
查看答案和解析>>【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,如果用反证法证明,应先假设__________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为做大旅游产业,在2015年投入资金3.2亿元,预计2017年投入资金6亿元,设旅游产业投资的年平均增长率为x,则可列方程为( )
A. 3.2+x=6B. 3.2x=6C. 3.2(1+x)=6D. 3.2(1+x)2=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:1﹣4a2=_____.
相关试题

