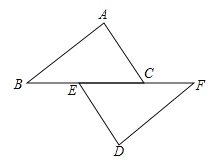
【题目】如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)9.
【解析】
试题分析:(1)首先证明△ABC≌△DFE可得∠ACE=∠DEF,进而可得AC∥DE;
(2)根据△ABC≌△DFE可得BC=EF,利用等式的性质可得EB=CF,再由BF=13,EC=5进而可得EB的长,然后可得答案.
试题解析:(1)证明:在△ABC和△DFE中,∵AB=DF,∠A=∠D,AC=DE,∴△ABC≌△DFE(SAS),∴∠ACE=∠DEF,∴AC∥DE;
(2)解:∵△ABC≌△DFE,∴BC=EF,∴CB﹣EC=EF﹣EC,∴EB=CF,∵BF=13,EC=5,∴EB=(13-5)÷2=4,∴CB=4+5=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个六棱柱的顶点个数、棱的条数、面的个数分别是( )
A. 6、12、6 B. 12、18、8
C. 18、12、6 D. 18、18、24
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和为1080°,则这个多边形的边数是 .
-
科目: 来源: 题型:
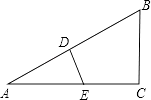
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E,△ABC的周长为12,△ADE的周长为6,则BC的长为( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
(1)根据题意,补全原形;
(2)求证:BE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=
 ,求
,求 的值.
的值.(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

-
科目: 来源: 题型:
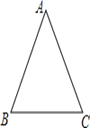
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
相关试题

