【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④![]() <a<
<a<![]()
⑤b>c.
其中含所有正确结论的选项是( )

A.①③ B.①③④ C.②④⑤ D.①③④⑤
参考答案:
【答案】D.
【解析】
试题分析:①由图象可知函数开口方向向上,可得a>0;由对称轴在原点左侧可得ab异号,再由抛物线与y轴交点在y轴负半轴可得c<0,所以abc>0,①正确;②由图象与x轴交于点A(﹣1,0),对称轴为直线x=﹣1,可得图象与x轴的另一个交点为(3,0),所以当x=2时,y<0,即4a+2b+c<0,②错误;③当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,所以a﹣b+c=0,即a=b﹣c,c=b﹣a,由对称轴为直线x=1可得![]() =1即b=﹣2a,即可得c=b﹣a=(﹣2a)﹣a=﹣3a,所以4ac﹣b2=4a(﹣3a)﹣(﹣2a)2=﹣16a2<0,再因8a>0,所以4ac﹣b2<8a,③正确;④由图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,可得﹣2<c<﹣1,所以﹣2<﹣3a<﹣1,即可得
=1即b=﹣2a,即可得c=b﹣a=(﹣2a)﹣a=﹣3a,所以4ac﹣b2=4a(﹣3a)﹣(﹣2a)2=﹣16a2<0,再因8a>0,所以4ac﹣b2<8a,③正确;④由图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,可得﹣2<c<﹣1,所以﹣2<﹣3a<﹣1,即可得![]() >a>
>a>![]() ;④正确;⑤因a>0,可得b﹣c>0,即b>c,⑤正确;故答案选:D.
;④正确;⑤因a>0,可得b﹣c>0,即b>c,⑤正确;故答案选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地连续九天的最高气温统计如下表:
最高气温(℃)
22
23
24
25
天数
1
2
2
4
则这组数据的中位数与众数分别是( )
A.24,25
B.24.5,25
C.25,24
D.23.5,24 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算结果为a7的是( )
A.(﹣a)2(﹣a)5
B.(﹣a)2(﹣a5)
C.(﹣a2)(﹣a)5
D.(﹣a)(﹣a)6 -
科目: 来源: 题型:
查看答案和解析>>【题目】当5个整数从小到大排列时,其中位数为4,如果这个数据组的唯一众数是6,则这5个整数可能的最大的和是( )
A.21
B.22
C.23
D.24 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为__________;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
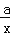 (a>0,a为常数)和y=
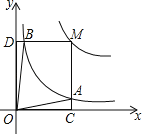
(a>0,a为常数)和y=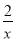 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=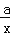 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=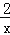 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=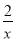 的图象于点B,当点M在y=
的图象于点B,当点M在y=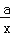 的图象上运动时,以下结论:
的图象上运动时,以下结论:①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
相关试题

