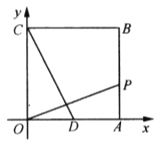
【题目】如图,点![]() 的坐标为
的坐标为![]() ,作
,作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上沿
上沿![]() 运动,当
运动,当![]() 时,点
时,点![]() 的坐标为________.
的坐标为________.
参考答案:
【答案】![]() 或
或![]()
【解析】
分两种情况①当点P在正方形的边AB上时,根据正方形的性质用HL判断出Rt△OCD≌Rt△OAP,得出AP=2,得出点P的坐标,②当点P在正方形的边BC上时,同①的方法即可.
①当点P在正方形的边AB上时,
在Rt△OCD和Rt△OAP中
![]() ,
,
∴Rt△OCD≌Rt△OAP,
∴OD=AP,
∵点D是OA中点,
∴OD=AD=![]() OA,
OA,
∴AP=![]() AB=2,
AB=2,
∴P(4,2),
②当点P在正方形的边BC上时,
同①的方法,得出CP=![]() BC=2,
BC=2,
∴P(2,4)
∴P(2,4)或(4,2)
故答案为(2,4)或(4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
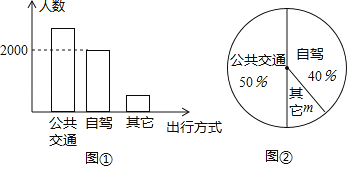
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)求证:BF⊥AF;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.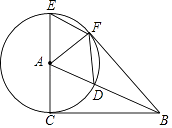
-
科目: 来源: 题型:
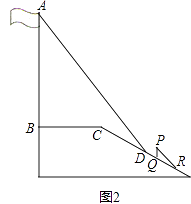
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示;
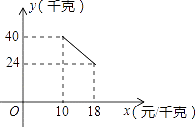
(1)求y(千克)与销售价x的函数关系式;
(2)该经销商想要获得150元的销售利润,销售价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图①中四边形
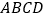 就是一个“格点四边形”.
就是一个“格点四边形”.(1)作出四边形
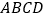 关于直线
关于直线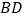 对称的四边形
对称的四边形 ;
;(2)图①中四边形
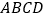 的面积是;
的面积是;(3)在图②方格纸中画一个格点三角形
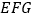 ,使
,使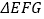 的面积等于8且
的面积等于8且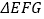 为轴对称.
为轴对称.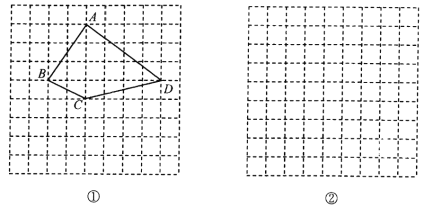
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
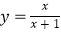 的图象与性质.小怀根据学习函数的经验,对函数
的图象与性质.小怀根据学习函数的经验,对函数 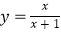 的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
的图象与性质进行了探究.下面是小怀的探究过程,请补充完成:
(1)函数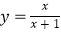 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)列出y与x的几组对应值.请直接写出m的值,m=;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数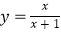 的一条性质.
的一条性质. x
…
﹣5
﹣4
﹣3
﹣2
﹣

﹣

0
1
2
m
4
5
…
y
…



2
3
﹣1
0



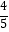

…
相关试题

