【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
参考答案:
【答案】(1)、证明过程见解析;(2)、①、△BOD′∽△AOC′,证明过程见解析;(2)、AC′=kBD′,∠AMB=α,证明过程见解析.
【解析】
试题分析:(1)、根据矩形的性质得出OA=OC=OB=OD,根据旋转可得OD=OD′,OC=OC′,∠D′OD=∠C′OC,根据平角得出∠BOD′=∠AOC′,从而说明三角形全等;(2)、根据平行四边形的性质得出OB=OD,OA=OC,根据旋转得出OD=OD′,OC=OC′,∠D′OD=∠C′OC,根据平角的性质得出∠BOD′=∠AOC′,从而得出三角形相似;根据三角形相似的性质进行说明.
试题解析:(1)、在矩形ABCD中,∵AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OA=OC=OB=OD,∵△D′OC′由△DOC旋转得到,∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB=OD′=OA=OC′,∴180°-∠D′OD=180°-∠C′OC, 即∠BOD′=∠AOC′,
∴△BOD′≌△AOC′
(2)、①猜想:△BOD′∽△AOC′.
∵在平行四边形ABCD中,OB=OD,OA=OC, ∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC, ∴OB:OA=OD′:OC′,180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′, ∴△BOD′∽△AOC′
②结论:AC′=kBD′,∠AMB=α
∵△BOD′∽△AOC′, ∴![]() ,即AC′=kBD′
,即AC′=kBD′
设BD′与AC相交于点N,∵△BOD′∽△AOC′,∴∠OBM=∠OAM,
在△ANM与△BNO中,又∵∠ANM=∠BNO,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,
即∠AMB=∠AOB=α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程ax-4=14x+a的解是x=2,则a的值是( )
A. 24 B. -24 C. 32 D. -32
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,则形成的几何体的体积是多少?(结果用π表示)
-
科目: 来源: 题型:
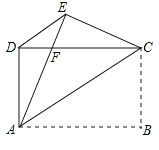
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;(2)求DF的值;(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】“神州五号”载人飞船绕地球飞行14圈,共飞行590200km,这个飞行距离用科学计数法表示为( )
A. 59.02×104km B. 0.5902×106km C. 5.902×105km D. 5.902×104km
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+2a﹣3=0,则代数式2a2+4a﹣3的值是( )
A. ﹣3 B. 0 C. 3 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y= -3x+5向上平移2个单位后得到的直线表达式是( )
A. y= -3x+2B. y= -3x-2C. y= -3x+7D. y= -3x-7
相关试题

