【题目】如图,AD为△ABC的中线,BE为三角形ABD中线, 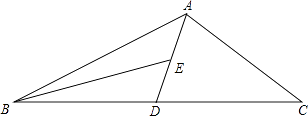
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
参考答案:
【答案】
(1)解:∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°
(2)解:如图所示,EF即是△BED中BD边上的高
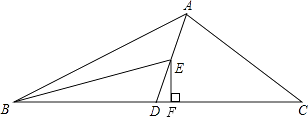
(3)解:∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△BED= ![]() S△ABC=
S△ABC= ![]() ×60=15;
×60=15;
∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6
【解析】(1)利用三角形的外角等于与它不相邻的两个内角之和即可求∠BED的度数;(2)△BED是钝角三角形,所以BD边上的高在BD的延长线上;(3)先根据三角形的中线把三角形分成面积相等的两个小三角形,结合题意可求得△BED的面积,再直接求点E到BC边的距离即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点
 ,
,  所对应的数是
所对应的数是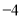 ,
, 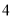 .
.对于关于
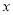 的代数式
的代数式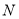 ,我们规定:当有理数
,我们规定:当有理数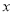 在数轴上所对应的点为
在数轴上所对应的点为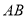 之间(包括点
之间(包括点 ,
, 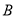 )的任意一点时,代数式
)的任意一点时,代数式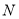 取得所有值的最大值小于等于
取得所有值的最大值小于等于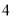 ,最小值大于等于
,最小值大于等于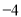 ,则称代数式
,则称代数式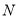 ,是线段
,是线段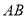 的封闭代数式.
的封闭代数式.例如,对于关于
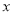 的代数式
的代数式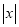 ,当
,当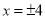 时,代数式
时,代数式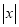 取得最大值是
取得最大值是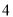 ;当
;当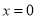 时,代数式
时,代数式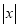 取得最小值是
取得最小值是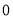 ,所以代数式
,所以代数式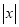 是线段
是线段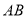 的封闭代数式.
的封闭代数式.问题:(
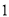 )关于
)关于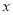 代数式
代数式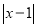 ,当有理数
,当有理数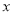 在数轴上所对应的点为
在数轴上所对应的点为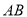 之间(包括点
之间(包括点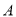 ,
, 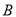 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.所以代数式
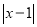 __________(填是或不是)线段
__________(填是或不是)线段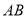 的封闭代数式.
的封闭代数式.(
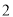 )以下关
)以下关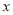 的代数式:
的代数式:①
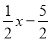 ;②
;②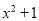 ;③
;③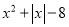 ;④
;④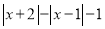 .
.是线段
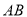 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段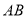 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).(
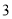 )关于
)关于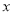 的代数式
的代数式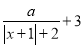 是线段
是线段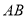 的封闭代数式,则有理数
的封闭代数式,则有理数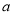 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.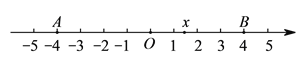
-
科目: 来源: 题型:
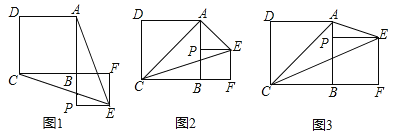
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣
 ﹣(+13)+(﹣
﹣(+13)+(﹣ )﹣(﹣17)
)﹣(﹣17)(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-14-(1-7)÷3×[(―3)2-3]
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市八年级8000名学生的体重情况,从中抽查了500名学生的体重进行统计分析,在这个问题中,样本容量是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)
相关试题

