【题目】如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.

(1)求证:AP是⊙O的切线;
(2)求PD的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)连接OA,利用等腰三角形的性质和角的关系求出∠OAP=90°,得出OA⊥AP即可;(2)连接AD,△ACD中利用tan30°求出AD=![]() ,然后证明∠P=∠PAD得出PD=AD=
,然后证明∠P=∠PAD得出PD=AD=![]() .
.
试题解析:(1)连接OA.
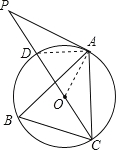
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=AC×tan30°=3×![]() =
=![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°,
∴∠P=∠PAD,
∴PD=AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在X轴、Y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在A’的位置,若OB=
 ,tan∠COB=
,tan∠COB= ,则点A’的坐标为______。
,则点A’的坐标为______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
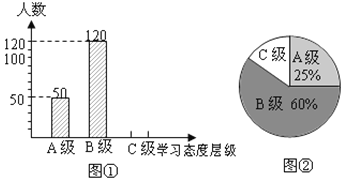
(1)此次抽样调查中,共调查了多少名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4= .
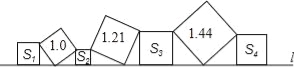
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种船,1艘大船与4艘小船一次可以载乘客46名,2艘大船与3艘小船一次可以载乘客57人.某船家有3艘大船与6艘小船,一次可以载游客的人数为( )
A.129 B.120 C.108 D.96
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xm-2-8yn+3=2是关于x,y的二元一次方程,则m+n的值是( )
A. 5 B. 4 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个两位数的个位数字与十位数字的和5,那么这样的两位数的个数是_________.
相关试题

