【题目】(本题10分)如图,已知二次函数![]() 的图象的顶点为A,二次函数
的图象的顶点为A,二次函数![]() 的图象与
的图象与![]() 轴交于原点O及另一点C,它的顶点B在函数
轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1) 求点A与点C的坐标;
(2) 当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

参考答案:
【答案】(1)A的坐标为(1,﹣2),C的坐标为(2,0).
(2)二次函数y=ax2+bx的关系式为y=﹣2x2+4x.
【解析】试题分析:(1)二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上,可知两个函数对称轴相等,因此先根据已知函数求出对称轴.根据函数解析式得出顶点A的坐标与对称轴,故可得出二次函数y=ax2+bx关于x=1对称,且函数与x轴的交点分别是原点和C点,所以点C和点O关于直线l对称,故可得出点C的坐标;
(2)因为四边形AOBC是菱形,根据菱形性质,可以得出点O和点C关于直线AB对称,点B和点A关于直线OC对称,因此,可求出点B的坐标,根据二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),将B,C代入解析式得出ab的值,进而得出其解析式.
试题解析:(1)∵y=x2-2x-1=(x-1)2-2,
∴顶点A的坐标为(1,-2).
∵二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
∴二次函数y=ax2+bx的对称轴为:直线x=1,
∴点C和点O关于直线x=1对称,
∴点C的坐标为(2,0).
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,
因此,点B的坐标为(1,2).
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以![]()
解得![]() ,
,
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.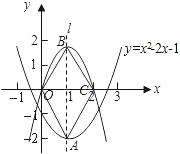
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题:
(1)a_________0;
(2)b_________0;
(3)b2﹣4ac_________0;
(4)y<0时,x的取值范围是_______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列图形:①线段;②平行四边形;③圆;④长方形;⑤等边三角形.其中,旋转对称图形是__________(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.
如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.
 B.
B.  C. 1 D. 0
C. 1 D. 0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的内角和是1800°,则这个正多边形的外角是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a5÷a3结果正确的是( )
A.a
B.a2
C.a3
D.a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)抛物线
 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与 轴交于点C.
轴交于点C.(1)求抛物线的解析式;
(2)如图1,P为线段AC上一点,过点P作
 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是
 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
图1 图2
相关试题

