【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1。
(2)若△ABC内有一点P(a,b),则经过(1)中的两次变换后点P的坐标变为_____________
(3)作出△ABC关于坐标原点O成中心对称的△A2B2C2.

参考答案:
【答案】(1)见解析;(2)(a+1,-b);(3)见解析.
【解析】
(1)根据网格结构找出点A、B、C关于x轴对称并向右平移1个单位后的对应点A1、B1、C1的位置,然后顺次连接即可;
(2)根据轴对称和平移的性质写出点P的对应点的坐标即可;
(3)根据网格结构找出点A、B、C关于原点O成中心对称的点A2、B2、C2的位置,然后顺次连接即可;
(1)如图所示;

(2)沿x轴翻折后点(a,b)坐标变为(a,-b),再沿x轴向右平移1个单位后则变为(a+1,-b),
故答案为:(a+1,-b);
(3)如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题
(1)抽取了______名学生成绩;(2)请把条形统计图补充完整;
(3)扇形统计图中等级D所在的扇形的圆心角度数是______;
(4)若A,B,C代表合格,该校初二年级有300名学生,求全年级生物合格的学生共约多少人

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:⑴□ABCD的周长;⑵线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是∠
是∠ 内的一点,过点
内的一点,过点 作
作 于点
于点 于点
于点 ,且
,且 .
. 求证:
求证:  ;
;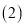 如图②,点
如图②,点 是射线
是射线 上一点,点
上一点,点 是线段
是线段 上一点,且
上一点,且 ,若
,若 .求线段
.求线段 的长.
的长. 如图③,若
如图③,若 ,将
,将 绕点
绕点 以每秒
以每秒 的速度顺时针旋转,
的速度顺时针旋转, 秒后,
秒后,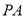 开始绕点
开始绕点 以每秒
以每秒 的速度顺时针旋转,
的速度顺时针旋转,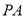 旋转
旋转 后停止,此时
后停止,此时 也随之停止旋转。旋转过程中,
也随之停止旋转。旋转过程中,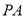 所在直线与
所在直线与 所在直线的交点记为
所在直线的交点记为 所在直线与
所在直线与 所在直线的交点记为
所在直线的交点记为 .问
.问 旋转几秒时,
旋转几秒时, ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证:
 ;
;(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线m:y=﹣0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段DE上一个动点(P不与D,E重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A,B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 _____________ ,(证明你的结论. )
(2)当四边形ABCD的对角线满足 __________条件时,四边形EFGH是矩形(不用证明)

相关试题

