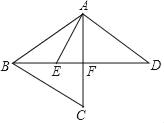
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.
参考答案:
【答案】6
【解析】
连接CE、CD,取DE的中点M,连接CM.首先证明△ECM,△ACD度数等边三角形,再证明△CEF∽△DEC即可解决问题.
解:连接CE、CD,取DE的中点M,连接CM.
∵AB=AC,∠EAB=∠EAC,AE=AE,
∴△EAB≌△EAC,
∴BE=EC=4,∠ABE=∠ACE,
∵AB=AD,
∴∠ABE=∠ADB,
∴∠ACE=∠ADF,
∵∠DFA=∠CFE,
∴∠DAF=∠CEF=60°,
∵EM=ED=4,
∴CE=EM,
∴△EMC是等边三角形,
∴CM=EM=DM,∠EMC=60°,
∵∠EMC=∠MCD+∠MDC,
∴∠MCD=∠MDC=30°,
∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∴∠ADB=∠ABD=∠ACE=∠CDB=30°,
∵∠CEF=∠CED,
∴△CEF∽△DEC,
∴EC2=EFED,
∴16=8EF,
∴EF=2,DF=DE﹣EF=6.
故答案为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究
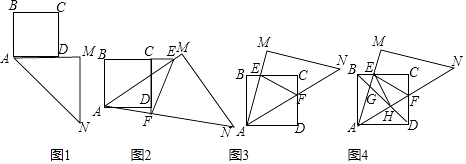
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN. -
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若
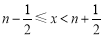 ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(
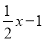 )=4,则实数x的取值范围是9≤x<11;
)=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2019x)=m+(2019x);
⑤(x+y)=(x)+(y);
其中,正确的结论有__________(填写所有正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.

(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.

(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3
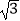 ),反比例函数y=
),反比例函数y= 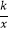 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )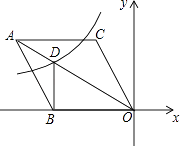
A.6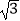
B.﹣6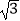
C.12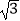
D.﹣12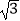
-
科目: 来源: 题型:
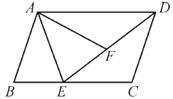
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的平分线,求证:
(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
相关试题

