【题目】小李的活鱼批发店以44元/公斤的价格从港口买进一批2000公斤的某品种活鱼,在运输过程中,有部分鱼未能存活,小李对运到的鱼进行随机抽查,结果如表一.由于市场调节,该品种活鱼的售价与日销售量之间有一定的变化规律,表二是近一段时间该批发店的销售记录.
(1)请估计运到的2000公斤鱼中活鱼的总重量;(直接写出答案)
(2)按此市场调节的观律,
①若该品种活鱼的售价定为52.5元/公斤,请估计日销售量,并说明理由;
②考虑到该批发店的储存条件,小李打算8天内卖完这批鱼(只卖活鱼),且售价保持不变,求该批发店每日卖鱼可能达到的最大利润,并说明理由.


参考答案:
【答案】(1) 估计运到的2000公斤鱼中活鱼的总重量为1760公斤;(2) ①可以估计当活鱼的售价定为52.5元/公斤时,日销售量为300公斤;②售价定为54.5元/公斤,每日卖鱼可能达到的最大利润为990元.
【解析】
(1)用总质量乘以0.880可得;
(2)①由表知,售价每增加1元,日销售量就减少40公斤,据此求解可得;
②由售价每增加x元/公斤,可估计日销售量在400公斤的基础上减少40x公斤,设批发店每日卖鱼的利润为w,根据总利润=每公斤的利润×销售量列出函数解析式,在根据题意求出增加的单价的取值范围,利用二次函数的性质求解可得.
(1) 估计运到的2000公斤鱼中活鱼的总重量为1760公斤;
(2) ①根据表二的销售记录可知,活鱼的售价每增加1元,其日销售量就减少40公斤,所以按此变化规律可以估计当活鱼的售价定为52.5元/公斤时,日销售量为300公斤;
②由(2) ①,若活鱼售价在50元/公斤的基础上,售价增加![]() 元/公斤,则可估计日销售量在400公斤的基础上减少40
元/公斤,则可估计日销售量在400公斤的基础上减少40![]() 公斤,
公斤,
设批发店每日卖鱼的最大利润为![]() ,
,
由题得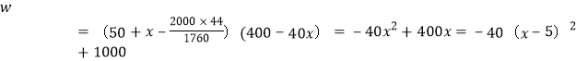
由“在8天内卖完这批活鱼”,可得![]() ,解得
,解得![]() .根据实际意义,有
.根据实际意义,有![]() ;解得
;解得![]() .
.
所以![]()
因为![]() ,
,
所以当![]() 时,
时,![]() 的增大而增大,
的增大而增大,
所以售价定为54.5元/公斤,每日卖鱼可能达到的最大利润为990元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的弦,P为AB的中点,连接OA、OP,将△OPA绕点O旋转到△OQB.设⊙O的半径为1,∠AOQ=135°,则AQ的长为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2+bx(b>2)上存在关于直线y=x成轴对称的两个点,则b的取值范围是______.
-
科目: 来源: 题型:
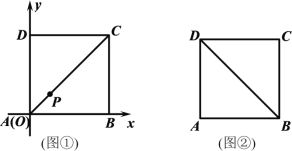
查看答案和解析>>【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=
 时,求点P的坐标;
时,求点P的坐标;(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
-
科目: 来源: 题型:
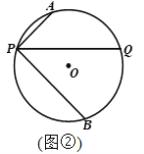
查看答案和解析>>【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2
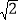 时,求⊙O的半径;
时,求⊙O的半径;(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为
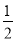
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
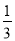
D.娜娜胜的概率和两人出相同手势的概率一样
相关试题

