【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.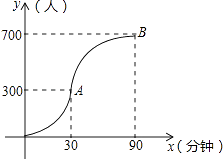
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
参考答案:
【答案】
(1)解:由图象可知,300=a×302,解得a= ![]() ,
,
n=700,b×(30﹣90)2+700=300,解得b=﹣ ![]() ,
,
∴y= 
(2)解:由题意﹣ ![]() (x﹣90)2+700=684,
(x﹣90)2+700=684,
解得x=78,
∴ ![]() =15,
=15,
∴15+30+(90﹣78)=57分钟
所以,馆外游客最多等待57分钟
【解析】(1)构建待定系数法即可解决问题;(2)先求出馆内人数等于684人时的时间,再求出直到馆内人数减少到624人时的时间,即可解决问题。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=
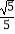 ,BD是AC边上的中线.求:
,BD是AC边上的中线.求: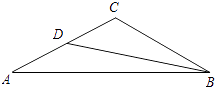
(1)△ABC的面积;
(2)∠ABD的余切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
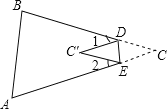
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图

(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)在x轴上是否存在点P,使得PA+PB最短,最短距离是多少?
(3)直接写出A1B1C1三点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发的960件新产品必须加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等,而且乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导.
(1)甲、乙两个工厂每天各能加工多少件产品?
(2)该公司要选择既省时又省钱的工厂加工产品,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,有望加工这批产品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
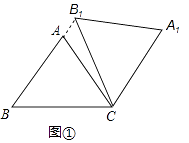
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.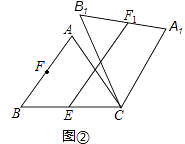
相关试题

