【题目】如图,已知AD是⊙O的直径,BC是⊙O的弦,AD⊥BC,垂足为点E,AE=BC=16,求⊙O的直径. 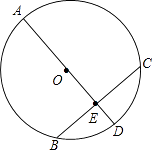
参考答案:
【答案】解: 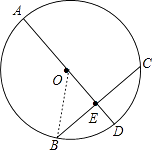
连接OB,设OB=OA=R,则OE=16﹣R,
∵AD⊥BC,BC=16,
∴∠OEB=90°,BE= ![]() BC=8,
BC=8,
由勾股定理得:OB2=OE2+BE2 ,
R2=(16﹣R)2+82 ,
解得:R=10,
即⊙O的直径为20
【解析】连接OB,根据垂径定理求出BE,根据勾股定理得出方程,求出方程的解即可.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠BAD=∠CDA,AB=DC=
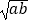 ,CE=a,AC=b,求证:
,CE=a,AC=b,求证: 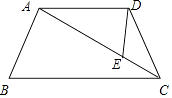
(1)△DEC∽△ADC;
(2)AEAB=BCDE. -
科目: 来源: 题型:
查看答案和解析>>【题目】一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)
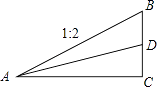
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知向量
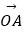 ,
, 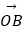 ,
, 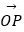 .
. 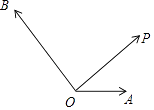
(1)求做:向量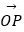 分别在
分别在 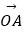 ,
, 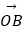 方向上的分向量
方向上的分向量  ,
, 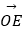 :(不要求写作法,但要在图中明确标出向量
:(不要求写作法,但要在图中明确标出向量  和
和 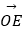 ).
).
(2)如果点A是线段OD的中点,联结AE、交线段OP于点Q,设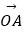 =
=  ,
, 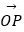 =
= 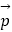 ,那么试用
,那么试用  ,
, 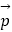 表示向量
表示向量 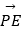 ,
, 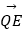 (请直接写出结论)
(请直接写出结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
-
科目: 来源: 题型:
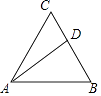
查看答案和解析>>【题目】如图,已知△ABC是边长为2的等边三角形,点D在边BC上,将△ABD沿着直线AD翻折,点B落在点B1处,如果B1D⊥AC,那么BD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
相关试题

