【题目】将下列各数填入相应的大括号内:
3.141 592 6,![]() ,
,![]() ,-6,8,
,-6,8,![]() ,2-π,0.014 545 454 5…,-
,2-π,0.014 545 454 5…,-![]() ,0,
,0,![]() ,0.323 223 222 3….
,0.323 223 222 3….
(1)有理数:{ …};
(2)无理数:{ …};
(3)正无理数:{ …};
(4)整数:{ …}.
参考答案:
【答案】(1)3.141 592 6,![]() ,-6,8,
,-6,8,![]() ,0.014 545 454 5…,0,
,0.014 545 454 5…,0,![]() ;(2)
;(2)![]() ,2-π,0.323 223 222 3…,-
,2-π,0.323 223 222 3…,-![]() ;(3)
;(3)![]() ,0.323 223 222 3…;(4)
,0.323 223 222 3…;(4)![]() ,-6,8,
,-6,8,![]() ,0.
,0.
【解析】
根据有理数是有限小数或无限循环小数,可得有理数集合;根据无理数是无限不循环小数,可得无理数集合;根据正无理数是正数中的无限不循环小数,可得正无理数集合;根据大于零的数是正数,整数包含正整数,负整数和0,可得整数集合.
(1)有理数:{3.141 592 6,![]() ,-6,8,
,-6,8,![]() ,0.014 545 454 5…,0,
,0.014 545 454 5…,0,![]() ,…}.
,…}.
(2)无理数:{![]() ,2-π,0.323 223 222 3…,-
,2-π,0.323 223 222 3…,-![]() ,…}.
,…}.
(3)正无理数:{![]() ,0.323 223 222 3…,…}.
,0.323 223 222 3…,…}.
(4)整数:{![]() ,-6,8,
,-6,8,![]() ,0,…}.
,0,…}.
-
科目: 来源: 题型:
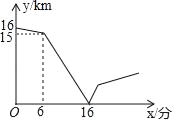
查看答案和解析>>【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(km)与甲出发的时间x(分)之间的关系如图所示.
(1)求甲、乙相遇时,乙所行驶的路程;
(2)当乙到达终点A时,甲还需多少分钟到达终点B?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
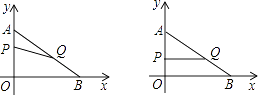
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为 个平方单位?
个平方单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=kx﹣3的图象如图所示,则一元二次方程x2+x+k﹣1=0根的存在情况是( )

A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )
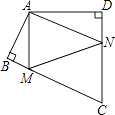
A.80°
B.90°
C.100°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x:
(1)16x2-361=0; (2)(x-1)2=25;
(3)27
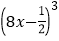 =216; (4)
=216; (4)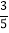 (x-2)3=
(x-2)3=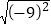 .
.
相关试题

