Question

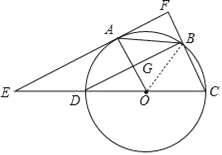
【题目】如图，已知⊙O的直径CD=6，A，B为圆周上两点，且四边形OABC是平行四边形。过A点作直线EF∥BD，分别交CD，CB的延长线于点E，F，AO与BD交于G点．

（1）求证：EF是⊙O的切线；

（2）求AE的长．

Answer 1

【答案】（1）证明见解析；（2）3.

【解析】试题分析：（1）利用圆周角定理得到∠DBC=90°，再利用平行四边形的性质得AO∥BC，所以BD⊥OA，加上EF∥BD，所以OA⊥EF，于是根据切线的判定定理可得到EF是⊙O的切线；

（2）连接OB，如图，利用平行四边形的性质得OA=BC，则OB=OC=BC，于是可判断△OBC为等边三角形，所以∠C=60°，易得∠AOE=∠C=60°，然后在Rt△OAE中利用正切的定义可求出AE的长．

试题解析：（1）证明：∵CD为直径，∴∠DBC=90°，∴BD⊥BC，

∵四边形OABC是平行四边形，∴AO∥BC，∴BD⊥OA，

∵EF∥BD，∴OA⊥EF，∴EF是⊙O的切线；

（2）解：连接OB，如图，∵四边形OABC是平行四边形，∴OA=BC，

而OB=OC=OA，∴OB=OC=BC，∴△OBC为等边三角形，∴∠C=60°，∴∠AOE=∠C=60°，

在Rt△OAE中，∵tan∠AOE=，∴AE=3tan60°=3．