【题目】已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
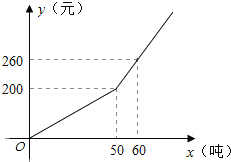
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收![]() 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
参考答案:
【答案】(1)y=kx+b(2)120吨(3)100吨
【解析】
试题分析:(1)设y关于x的函数关系式y=kx+b,代入(50,200)、(60,260)两点求得解析式即可;
(2)把y=620代入(1)求得答案即可;
(3)利用水费+污水处理费=600元,列出方程解决问题.
解:(1)设y关于x的函数关系式y=kx+b,
∵直线y=kx+b经过点(50,200),(60,260)
∴![]()
解得![]()
∴y关于x的函数关系式是y=6x﹣100;
(2)由图可知,当y=620时,x>50,
∴6x﹣100=620,
解得x=120.
答:该企业2013年10月份的用水量为120吨.
(3)由题意得6x﹣100+![]() (x﹣80)=600,
(x﹣80)=600,
化简得x2+40x﹣14000=0
解得:x1=100,x2=﹣140(不合题意,舍去).
答:这个企业2014年3月份的用水量是100吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=45°,∠B=46°,那么△ABC的形状为( )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲型H1N1流感病毒的直径约是0.00000011米,用科学记数法表示为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
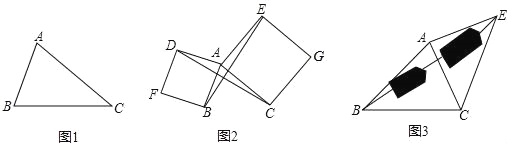
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
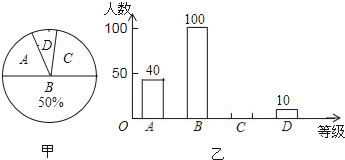
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(x﹣1)2﹣4,当y<0时,x的取值范围是( )
A. ﹣3<x<1 B. x<﹣1或x>3 C. ﹣1<x<3 D. x<﹣3或x>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
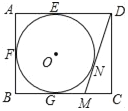
A.
 B.
B.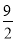 C.
C.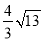 D.
D.
相关试题

