【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.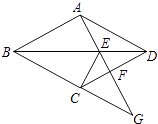
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
参考答案:
【答案】
(1)
证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
 .
.
∴△ADE≌△CDE,
∴∠DAE=∠DCE.
(2)FG=3EF
【解析】(2.)解:理由:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
由题意知:△ADE≌△CDE
∴∠DAE=∠DCE,
则∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴ ![]() =
= ![]() ,
,
∵EC=2EF,
∴ ![]() =
= ![]() ,
,
∴EG=2EC=4EF,
∴FG=EG﹣EF=4EF﹣EF=3EF.
故答案为FG=3EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AD 是高,∠BAD=60°,∠CAD=20°,AE 平分∠BAC,则∠EAD 的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某房产开发公司对一幢住宅楼的标价是:基价2580元/平方米,楼层差价如下表:

老王买了面积为80平方米的三楼.
(1)问老王花了多少钱?
(2)若他用同样多的钱去买六楼,请你帮老王算一算他可以多买多少平方米的房子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
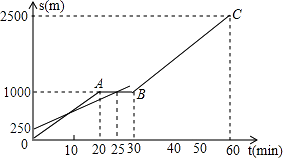
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).
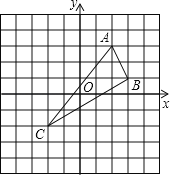
(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;
(2)求四边形ABED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E,使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断.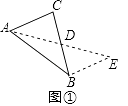
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连结EF.请判断BE+CF与EF的大小关系,并说明理由.
相关试题

