【题目】已知关于![]() 的方程x2-(2k+1)x+4k-2=0
的方程x2-(2k+1)x+4k-2=0
(1)求证:不论k取何值,这个方程总有实数根
(2)若等腰△ABC一边长a=4,另两边长b,c恰好是这个方程的两根,求△ABC的周长.
参考答案:
【答案】(1)证明见解析;(2)10.
【解析】(1)根据方程各项的系数利用根的判别式即可得出=(2k-3)2≥0,此题得证;
(2)当a为底时,则b、c为腰,根据两根相等得出k的值;当a为腰时,则b、c中有一个的值也等于4,将其代入方程求出k的值;再根据根与系数的关系求出a+b的值,进而可求出三角形的周长.
(1)证明:∵在方程x2-(2k+1)x+4k-2=0中,
△=[-(2k+1)]2-4(4k-2)=4k2-12k+9=(2k-3)2≥0,
∴不论k取什么实数值,这个方程总有实数根;
(2)解:当a为底边时,b=c,
∴△=(2k-3)2=0,解得:k=![]() ,
,
∴b+c=2k+1=4=a,
∴此种情况不合适;
当a为腰时,将x=4代入原方程得:16-4(2k+1)+4k-2=0,
解得:k=![]() .
.
∴b+c=2k+1=6,
∴△ABC的周长=a+b+c=4+6=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,O是对角线的交点,AF平分
 BAC,DH
BAC,DH AF于点H,交AC于G,DH延长线交AB于点E,求证:BE=2OG.
AF于点H,交AC于G,DH延长线交AB于点E,求证:BE=2OG.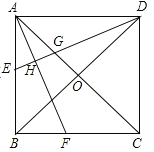
-
科目: 来源: 题型:
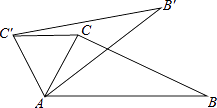
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
A.70°
B.35°
C.40°
D.50° -
科目: 来源: 题型:
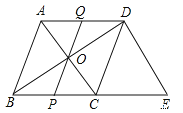
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于O点,AB=5,AC=6,过D点作DE//AC交BC的延长线于E点
(1)求△BDE的周长
(2)点P为线段BC上的点,连接PO并延长交AD于点Q,求证:BP=DQ
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》“勾股”章的问题::“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙各行几何?”大意是说:如图,甲乙二人从A处同时出发,甲的速度与乙的速度之比为7:3,乙一直向东走,甲先向南走十步到达C处,后沿北偏东某方向走了一段距离后与乙在B处相遇,这时,甲乙各走了多远?
相关试题

