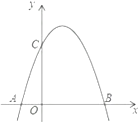
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
参考答案:
【答案】(1)y=-x2+2x+3;(2)(1,4); (3)P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.
【解析】试题分析:
(1)由题意可设该抛物线的解析式为![]() ,代入点(-1,0)求出k的值即可得到所求解析式;
,代入点(-1,0)求出k的值即可得到所求解析式;
(2)由(1)中所得抛物线的解析式可求得点B、C的坐标,从而可求出直线BC的解析式,由直线NC⊥BC且过点C可求得NC的解析式,把NC的解析式和抛物线的解析式联立得到方程组,解方程组即可求得点N的坐标;
(3)如下图,由题意易得PQ=OA=1,且PQ∥OA,设点P的横坐标为t,则可用含“t”的式子表达出Q的坐标,再把Q的坐标代入函数y=![]() x+
x+![]() 中,即可解得“t”的值,从而可求得P、Q的坐标.
中,即可解得“t”的值,从而可求得P、Q的坐标.
试题解析:
(1)设抛物线的解析式是y=-(x-1)2+4.把 (-1,0)代入得 0=-(1-1)2+k,
解得,k=4
则抛物线的解析式是 y=-(x-1)2+4,
即y=-x2+2x+3;
(2)设直线BC的解析式为y=kx+b(k≠0),代入点B、C的坐标得:
![]() 解得:
解得: ![]() ,
,
∴直线BC的解析式为:y=-x+3,
∵BC⊥NC,
∴可设直线CN的解析式为y=x+m.
∵C(0,3)在直线CN上,
∴0+m=3,解得:m=3,即直线CN的解析式为 y=x+3,
由: ![]() ,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
∴N的坐标是(1,4),

(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1, -t2+2t+3) ,将P、Q的坐标代入![]() ,
,
得-t2+2t+3=![]() ,
,
整理,得2t2-t=0, ,
解得t=0 或![]() .
.
∴-t2+2t+3 的值为3或![]() .
.
∴P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
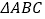 中,
中, ,
, ,
, 与
与 相交于点
相交于点 ,且
,且 ,
, ,垂足分别为点
,垂足分别为点 、
、 .
.
(1)若
 ,
, ,求
,求 的长.
的长.(2)如图2,取
 中点
中点 ,连接
,连接 、
、 ,请判断
,请判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两个可以自由转动的转盘,每个转盘分成三个相同的扇形,涂色情况如图所示,指针的位置固定,同时转动两个转盘,回答以下问题:

圆1 圆2
圆2
圆1
(1)补全表格:圆1的所有可能结果有 种,分别是 ;
圆2的所有可能结果有 种,分别是 .
(2)写出:转盘停止后指针指向同种颜色区域的概率和至少有一指针指向红色区域的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点
,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 处,并按
处,并按 的规律紧绕在四边形
的规律紧绕在四边形 的边上,则细线另一端所在位置的点的坐标是( )
的边上,则细线另一端所在位置的点的坐标是( )
A.
 B.
B. C.
C. D.
D.
相关试题

