【题目】感知:如图①,在矩形ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在矩形ABCD内部的点F处,延长AF交CD于点G,连结FC,易证∠GCF=∠GFC.
探究:将图①中的矩形ABCD改为平行四边形,其他条件不变,如图②,判断∠GCF=∠GFC是否仍然相等,并说明理由.
应用:如图②,若AB=5,BC=6,则△ADG的周长为 .

参考答案:
【答案】探究:∠GCF=∠GFC,理由见解析;应用:16.
【解析】
试题分析:探究:由ABCD及折叠可得∠B+∠ECG=∠AFE+∠ECG=∠AFE+∠EFG=180°,即∠ECG=∠EFG,再根据EB=EF=EC得∠EFC=ECF,从而可得∠GCF=∠GFC;
应用:由(1)中∠GCF=∠GFC得GF=GC,AF=AB,根据△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD可得.
试题解析:探究:∠GCF=∠GFC,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠ECG=180°,
又∵△AFE是由△ABE翻折得到,
∴∠AFE=∠B,EF=BE,
又∵∠AFE+∠EFG=180°,
∴∠ECG=∠EFG,
又∵点E是边BC的中点,
∴EC=BE,
∵EF=BE,
∴EC=EF,
∴∠ECF=∠EFC,
∴∠ECG-∠ECF=∠EFG-∠EFC,
∴∠GCF=∠GFC;
应用:∵△AFE是由△ABE翻折得到,
∴AF=AB=5,
由(1)知∠GCF=∠GFC,
∴GF=GC,
∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A. x2+2x2=3x4 B. (﹣2x2)3=8x6 C. x2(﹣x3)=﹣x5 D. 2x2÷x2=x
-
科目: 来源: 题型:
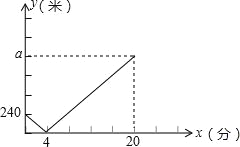
查看答案和解析>>【题目】小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.
(1)小明每分钟步行 米,a= ,小明家离图书馆的距离为 米.
(2)在图中画出小亮离学校的距离y(米)与x(分)之间的函数图象.
(3)求小明和小亮在途中相遇时二人离图书馆的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5cm,直线1上有一点P,OP=5cm,则直线1与⊙O的位置关系为( )
A. 相交 B. 相离 C. 相切 D. 相交或相切
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式是( )
A. 2m+3n=12B. m+n=8C. 2m+n=6D. m+2n=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果正多边形的一个内角是144°,则这个多边形是( )
A.正十边形
B.正九边形
C.正八边形
D.正七边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3、-2、0、1、4的中位数是( )
A. 0B. 1C. -2D. 4
相关试题

